11.2. ЗАДАЧА ОПТИМИЗАЦИИ ПОРТФЕЛЯ
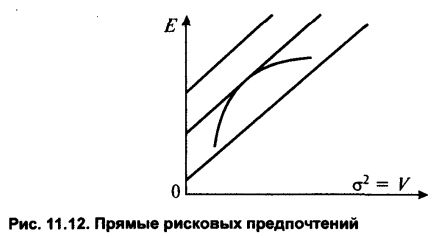
Для того чтобы составить эффективный портфель, необходимо найти точку касания границы эффективности с кривой безразличия инвестора (рис. 11.12). Предположим, инвестор намечает иметь в портфеле N определенных ценных бумаг. Ему необходимы характеристики этих бумаг, т.е. ожидаемые доходности Е/, риск а„ и знать или вычислить коэффициенты корреляции Гу между всеми парами выбранных бумаг. Для удобства дальнейшего описания будем пользоваться ковариациями Cv = PyOjGj. В сумме необходимо найти N + N2 величин.
Далее, перейдем от системы координат (?, ст) к системе координат (Е, V). В наших осях парабола, характеризующая кривую безразличия инвестора, будет выглядеть прямой.
Запишем уравнение для семейства прямых безразличия в виде:
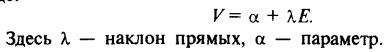
Стремясь достичь максимальной полезности, инвестор окажется на прямой с минимально возможным значением а. Следовательно, перед инвестором стоит задача найти такие Xh при которых минимально
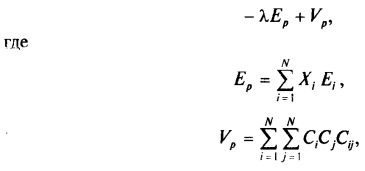
при условии 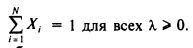 Надо сказать, что Xt могут принимать любые значения в интервале (—оо, +оо). Отрицательная величина X, означает, что ценные бумаги с соответствующими характеристиками нужно не покупать, а продавать. Будем искать решение для X, в виде Xtf = Kt + ktX. Тогда, решив задачу однажды, можно, меняя рисковые предпочтения, подбирать нужный портфель (рис. 11.13). Например, инвестор хочет создать портфель из трех бумаг. В результате решения он получит такую, например, картину: Надо сказать, что Xt могут принимать любые значения в интервале (—оо, +оо). Отрицательная величина X, означает, что ценные бумаги с соответствующими характеристиками нужно не покупать, а продавать. Будем искать решение для X, в виде Xtf = Kt + ktX. Тогда, решив задачу однажды, можно, меняя рисковые предпочтения, подбирать нужный портфель (рис. 11.13). Например, инвестор хочет создать портфель из трех бумаг. В результате решения он получит такую, например, картину:
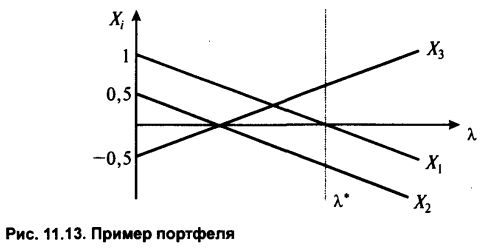
Выбрав цену риска, соответствующую к*, инвестор получит эффективный портфель, отвечающий его готовности рисковать ради получения дохода. Тогда
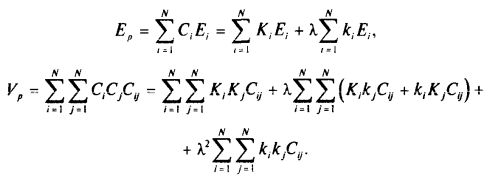
Задача, подобная описанной, решается методом Лагранжа. Полагая, что читатель с этим методом знаком, приведем получающуюся в результате его применения систему линейных уравнений:
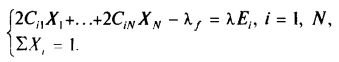
Эту систему необходимо решить дважды. Сначала принять X = 0, тогда получится Kh будет описан портфель с минимальной вариацией, а затем решить эту же систему, задав, например, X = 1. Тогда получим kh и задача решена для любых X.
Рассмотрим пример. Пусть инвестор хочет создать портфель из трех акций, имеющих следующие характеристики:
— ожидаемые доходности — 20%, 30% и 40%;
— стандартные отклонения — 20%, 40% и 50% соответственно;
— коэффициенты корреляции —

Пусть на рынке есть безрисковые бумаги с ?, = 10% и, конечно, о, = 0. Тогда, если составить портфель из безрисковой ценной бумаги и первых двух из предыдущего портфеля, получим систему уравнений:
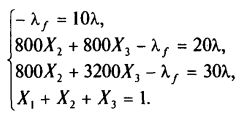
Повторив уже описанную процедуру, получим следующее решение:
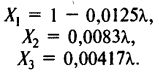
Обратите внимание на то, что для рискованных ценных бумаг К = 0. Это общее свойство решения системы уравнений при наличии в портфеле безрисковой ценной бумаги.
|