Существует ли оптимальное f?
Оптимальность f в смысле максимизации капитала видна из того, что:
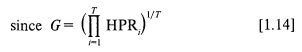
и
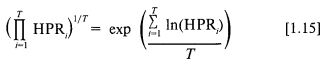
Отсюда, согласно закону больших чисел в слабой форме или Центральной предельной теоремы теории вероятностей применительно к сумме независимых переменных (т. е. к числителю правой части выражения [1.15]), если максимизировать среднее геометрическое по всем периодам владения на достаточно большой выборке данных, то почти наверняка получим больший конечный капитал, чем с помощью любого другого решающего правила.
Кроме того, для доказательства оптимальности f мы можем также воспользоваться теоремой Ролля. Вспомните, что под оптимальностью мы понимаем то, что дает наибольший геометрический рост с увеличением количества испытаний. Поскольку показателем среднего геометрического роста является TWR, нам нужно доказать, что существует такое значение f, при котором достигается максимум TWR.


Теорема Ролля утверждает, что если некая функция пересекает линию, параллельную оси х в двух точках а и b, и функция непрерывна на интервале [а, b], то на этом интервале существует по крайней мере одна точка, в которой первая производная этой функции обращается в нуль (т. е. имеется по крайней мере один относительный экстремум).
Поскольку все функции с положительным арифметическим математическим ожиданием пересекают ось х дважды (в качестве оси х выступает ось f), при f = 0 и в той точке справа, где f дает такие расчетные HPR, что их дисперсия превосходит среднее арифметическое HPR минус один. Эти две точки будут определять наш интервал [а, b] на оси х. Далее, первая производная фундаментального уравнения торговли (т. е. оценочного TWR) будет непрерывна при всех f внутри данного интервала, поскольку /дает такие значения AHPR и дисперсии HPR внутри интервала, которые дифференцируемы на нем. Следовательно, оценочное TWR как функция от f непрерывна внутри интервала. Значит, согласно теореме Ролля, на этом интервале должен быть по крайней мере один относительный экстремум. Поскольку на этом интервале оценочное TWR положительно, то есть расположено над осью х, на нем должен содержаться, по меньшей мере, один максимум.
Фактически, на этом интервале может быть лишь один максимум, так как изменение среднего геометрического HPR (среднее геометрическое HPR является корнем степени Т из TWR), согласно теореме Пифагора, впрямую зависит от AHPR и дисперсии, когда оба они при изменении f изменяются в противоположных направлениях. Этим гарантируется единственность вершины. Таким образом, на данном интервале должен быть максимум, и он может быть только один.
Теперь вернемся к уравнению [1.06] и вновь рассмотрим игру в монетку с выплатой «два-к-одному». У нас имеется две сделки, или два возможных сценария. Взяв первую производную от [1.06] по f, получим:
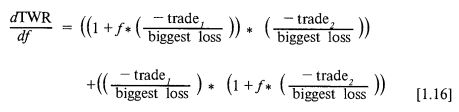
При количестве сделок большем двух можно использовать эту же формулу, но она сразу же сильно разрастается. Поэтому для простоты мы остановимся лишь на двух сделках. В этих условиях для серии исходов +2, -1 при f = 0,25 будем иметь:
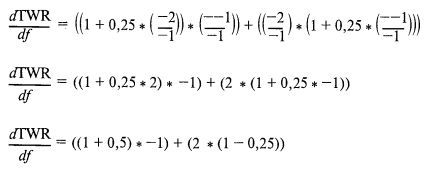
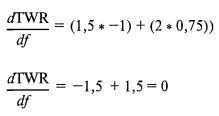
Как видим, функция достигает вершины при f = 0,25, где наклон касательной равен нулю, то есть точно при оптимальном f, и никакого другого локального экстремума существовать не может из-за ограничений, накладываемых теоремой Пифагора.
Наконец, покажем, что оптимальное f не зависит от Т. Взяв первую производную от оценочного TWR в форме [1.13] по переменной Т, получим:
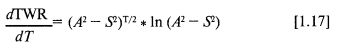
Поскольку ln (1) = 0, то при том значении f, когда А2 – S2 = 1, функция достигает вершины – максимума TWR, зависящего лишь от f. Отметим также, что и А (среднее арифметическое HPR) и S (стандартное отклонение этих HPR) не является функциями от Т – они не зависят от него. Поэтому [1.13] не зависит от Т при оптимальном f. То f, которое оптимально в смысле максимизации оценочного TWR, всегда будет иметь одно и то же значение, независимо от Т.
|