Сценарное планирование
Все, кто зарабатывает прогнозированием, будь то экономисты, аналитики рынка акций, метеорологи, госслужащие и т. д., неизбежно когда-то ошибаются. Но от этого никуда не уйти, ибо большинство решений, которые должны приниматься человеком в жизни, обычно требуют от него прогноза будущего.
Наше прогнозирование страдает как минимум двумя очевидными недостатками. Начнем с того, что человеку свойственно делать более оптимистичные предположения о будущих событиях, чем их реальные вероятности. Большинство людей считает, что у них есть куда больше шансов выиграть в лотерею в этом месяце, чем погибнуть в автокатастрофе, хотя вероятность последнего выше. Это справедливо не только в отношении отдельных лиц, но еще более выражено на групповом уровне. Работая вместе, люди склонны считать благоприятные исходы более вероятными.
Второй, и еще более пагубный недостаток, состоит в том, что люди прогнозируют будущее прямолинейно. Они предсказывают, какой будет цена галлона бензина двумя годами позже, что будет с их работой, кто будет следующим президентом, какими будут моды и так далее, и так далее. Задумываясь о будущем, мы склонны рассматривать его как единственный наиболее вероятный исход. В результате, как только нужно принять решение и на индивидуальном, и на групповом уровне, мы склонны опираться на то, что, по нашему мнению, будет единственным наиболее вероятным исходом в будущем. Вследствие этого, мы становимся беззащитными перед неприятными сюрпризами.
Сценарное планирование дает частичное решение этих проблем. Сценарий представляет собой один из возможных прогнозов, описание одного из путей, которым могут пойти события в будущем. Сценарное планирование нацелено на составление набора сценариев, покрывающего определенный спектр возможностей. Разумеется, охватить весь спектр возможностей нереально, поэтому планировщик сценариев желает учесть их по максимуму. Действуя таким образом, в отличие от линейного прогнозирования наиболее вероятного исхода, планировщик сценария может приспосабливаться к будущим событиям, куда бы они ни повернули. Более того, сценарное планирование позволяет планировщику подготовиться к тому, что в ином случае стало бы неожиданностью. Сценарное планирование согласуется с реальной жизнью, ибо оно исходит из иллюзорности нашего детерминизма.
Предположим, что в ваши обязанности входит участие в долгосрочном планировании для вашей компании, которая производит какой-то конкретный продукт. Вместо того чтобы положиться на единственный наиболее вероятный линейный прогноз, вы решаете заняться сценарным планированием. Вы усаживаетесь вместе с другими планировщиками и методом «мозговой атаки» принимаетесь вырабатывать возможные сценарии. Что, если у вас не хватит сырья для производства вашего продукта? Что, если одного из ваших конкурентов постигнет неудача? Что, если появится новый конкурент? Что, если вы серьезно недооцените спрос на ваш продукт? Что, если на каком-либо континенте разгорится война? И что, если она будет ядерной?
Поскольку каждый сценарий представляет лишь одну из возможностей, его можно основательно проработать. Но что делать после того, как вы проделали это для всех своих сценариев?
Для начала вы должны определить, какую цель вы хотели бы достичь в каждом из сценариев. Эта цель зависит от сценария и не обязана быть прогрессивной. Например, при негативном сценарии ваша цель может состоять просто в поддержании живучести компании. Определившись с целью по каждому сценарию, вы должны будете выработать планы достижения вашей цели в случае реализации данного сценария. Например, на случай маловероятного негативного сценария, когда ваша цель – остаться на плаву, нужно иметь планы, позволяющие минимизировать ущерб. Главное преимущество сценарного планирования состоит в том, что оно вооружает вас конкретным образом действий на случай определенного развития событий. Оно принуждает вас к составлению планов до того, как произойдут те или иные события, заставляет подготовиться к неожиданностям.


Впрочем, сценарное планирование позволяет добиться много большего. Оно тесно взаимосвязано с оптимальным f, что дает возможность оптимально распределять инвестиции между компонентами сценарного набора. Хотя мы и закладываемся на многовариантное развитие событий в будущем, жизнь всегда выбирает какой-то один сценарий. Поэтому при сценарном планировании нам нередко приходится согласовывать текущее инвестирование с возможными сценариями завтрашнего дня. В этом проявляется подлинная суть сценарного планирования – его нацеленность на количественное осмысление будущего.
Прежде всего, мы должны описать каждый сценарий по отдельности. Затем мы должны сопоставить ему вероятность его реализации. Вероятность – это число между 0 и 1. Нам не нужно рассматривать такие сценарии, вероятность реализации которых равна 0. Кроме того, сопоставляемые вероятности не носят интегрального характера. Другими словами, каждому сценарию отвечает своя вероятность. Предположим, что мы планируем деятельность некоторой промышленной компании. При этом согласно одному из множества отслеживаемых сценариев наша компания с вероятностью 0,15 будет привлечена к суду за банкротство, а согласно другому – с верояностью 0,07 разорится в результате острой иностранной конкуренции. Теперь мы должны задаться вопросом, не является ли первый сценарий (привлечение к суду за банкротство) следствием второго сценария (банкротство в результате острой иностранной конкуренции). Если это так, тогда из вероятности первого сценария нужно исключить вероятность второго сценария, то есть понизить вероятность первого сценария до 0,08 (0,15-0,07).
Не менее важным, чем уникальность вероятностей сценариев, является другое требование: сумма вероятностей всех рассматриваемых сценариев должна быть строго равна 1. То есть она не может быть равна ни 1,01, или 0,99, а только 1.
Теперь, когда каждому сценарию сопоставлена вероятность реализации, нам нужно сопоставить ему его исход. Это – численная величина. Она может выражать заработанные или потерянные деньги в результате реализации сценария, количество единиц какого-то средства, лекарства или еще чего-то. Требуется лишь, чтобы исход измерялся в тех же единицах, в которых выражаются наши инвестиции.
Для использования данного метода нужно, чтобы хотя бы у одного сценария был отрицательный исход. Это – обязательное требование.
Последним требованием данного метода является положительность математического ожидания, т. е. суммы произведений исходов на их вероятности (формула [1.01]). Если математическое ожидание равно нулю или отрицательно, то излагаемый ниже метод применять нельзя. Это не значит, что нельзя использовать сценарное планирование как таковое. Его можно и нужно использовать. Но оптимальное f может работать в рамках сценарного планирования только при положительном математическом ожидании.
Кроме перечисленного, нужно стараться охватить как можно большую часть спектра возможных исходов. Другими словами, очень желательно, чтобы было учтено 99% возможных исходов. Это может показаться почти нереальным, но поскольку многие сценарии можно расширить, то для покрытия 99% спектра вам не понадобятся 10000 сценариев.
Расширяя сценарии, следует избегать типичной ошибки планирования трех вариантов: одного оптимистического сценария, другого пессимистического и третьего, сохраняющего положение неизменным. Это – слишком просто, и вытекающие отсюда решения часто слишком грубы для того, чтобы хоть чем-то помочь. Ведь вы же не станете ограничиваться только тремя сделками при определении оптимального f своей торговой системы?
Итак, даже если для охвата всего спектра исходов нужно запредельное количество сценариев, то 99% спектра покрыть вполне реально. Когда количество сценариев превосходит наши операционные возможности, можно расширять сценарии, тем самым уменьшая их количество. Однако, действуя подобным образом, мы теряем некое количество информации. Если мы сокращаем количество сценариев (расширяя их) только до трех (типичная ошибка), то безвозвратно теряем так много информации, что это серьезно снижает эффективность данного метода.
Спрашивается, какое количество сценариев будет достаточным? Оно должно быть как можно больше, но не превосходить ваших операционных возможностей. При необходимости их можно расширить с помощью компьютера.
Представим нашу орлянку «два-к-одному» в виде спектра из двух сценариев. Один из них предусматривает выпадение орла, а другой – решки. Они равновероятны (по 0,5) и имеют исходы +2 и —1, соответственно. То есть:

Предположим, что мы вновь планируем деятельность промышленной компании на основе продаж какого-то своего продукта в отдаленной и слаборазвитой карликовой стране. Предположим далее, что мы отслеживаем всего пять возможных сценариев (в реальности их было бы гораздо больше, но для простоты мы ограничимся пятью). Эти пять сценариев отражают наше видение возможного будущего данной страны, вероятности их реализации, а также прибыли и потери от инвестирования:
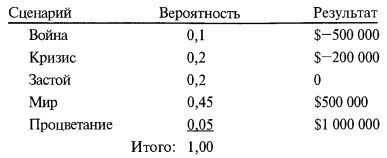
Сумма наших вероятностей равна 1. По крайней мере исход одного сценария отрицателен, а математическое ожидание положительно:
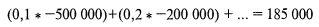
Следовательно, к этому сценарному набору можно применить наш метод.
Заметим для начала, что если бы мы заложились на единственный наиболее вероятный исход, то пришли бы к выводу, что мир – это и есть будущее данной страны, и стали бы действовать так, как если бы мир уже воцарился (как непреложный факт), и лишь смутно осознавая прочие возможности.
Следуя нашему методу, мы должны определить оптимальное f. Оно представляет собой такое значение f (между нулем и единицей), которое максимизирует среднее геометрическое в выражениях [1.20-1.22]. Далее, используя формулу [1.21], получаем значение относительного конечного капитала, или TWR. Наконец, взяв корень степени Σpi от [1.21], получим средний общий прирост на игру, или среднее геометрическое HPR. Для этого воспользуемся формулой [1.22].
Такова последовательность применения наших формул. Но для начала нужно выбрать схему оптимизации, или способ перебора значений f, который приводит к такому f, которое максимизирует выражения [1.20—1.22]. Для этого мы можем, как и раньше, воспользоваться прямым перебором значений f от 0,01 до 1, или прибегнуть к параболической интерполяции.
Затем мы должны определить наихудший возможный результат по сценарию среди всех отслеживаемых нами сценариев, какой бы малой ни была вероятность его реализации. В примере с промышленной компанией наихудшим результатом будет – 500000 долл.
Теперь для каждого возможного сценария нужно разделить наихудший возможный результат на значение f с минусом. В нашем примере с промышленной компанией мы будем предполагать, что эта процедура выполняется в ходе перебора значений f от 0,01 до 1. Поэтому мы начинаем со значения f, равного 0,01. То есть мы делим наихудший возможный исход отслеживаемых сценариев на значение f с минусом и получаем:
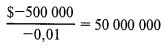
Заметьте, что деление отрицательной величины на отрицательную величину дает положительный результат, и наоборот. Поэтому в данном случае наш результат положителен. Теперь, переходя от сценария к сценарию, мы будем делить его исход на только что полученную величину. Поскольку исход первого сценария является также и самым худшим (потеря 500000 долл.), для него получаем:
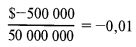
На следующем шаге прибавляем эту величину к 1. Это дает нам:
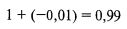
Наконец, возводим полученный результат в степень, равную вероятности реализации сценария, которая в нашем примере равна 0,1:
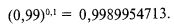
Далее переходим к следующему сценарию, названному Кризисом, который, реализуясь с вероятностью 0,2, приносит потерю 200000 долл. Наш результат худшего случая остается прежним: -500000 долл. Раз мы используем для f прежнее значение 0,01, то и величина, на которую нужно делить результат данного сценария, будет по-прежнему равна 50 миллионам:
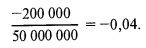
Проделав оставшиеся шаги, получим наше HPR:
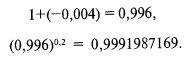
Продолжив перебор сценариев при тестируемом значении f = 0,01, получим значения HPR, соответствующих трем последним сценариям:

Преобразовав каждый сценарий в его HPR для данного значения f, перемножим эти HPR между собой и получим:

Эта дает нам промежуточное значение TWR, которое в данном случае равно 1,003667853. Нашим следующим шагом будет возведение этого числа в степень, равную единице, деленной на сумму вероятностей сценариев. Поскольку эта сумма всегда равна 1, можно утверждать, что, возведя TWR в степень 1, мы должны получить среднее геометрическое. Так как возведение любого числа в степень 1 равняется ему самому, можно сказать, что в данном случае наше среднее геометрическое равно TWR. То есть оно равно 1,003667853.
Если снять требование, что каждому сценарию соответствует своя, уникальная вероятность, то мы можем допустить, что сумма вероятностей больше 1. В таком случае для получения среднего геометрического нам пришлось бы возвести наше TWR в степень, равную 1, деленной на эту сумму вероятностей.
Мы только что получили среднее геометрическое, которое соответствует f = 0,01. Теперь перейдем к f = 0,02, и повторим весь процесс вплоть до получения соответствующего среднего геометрического. Будем действовать таким образом, пока не найдем такое f, которое дает самое большое среднее геометрическое.
В нашем примере оказывается, что максимум среднего геометрического, равный 1,1106, достигается при f = 0,57. Разделив худший исход по сценариям (—500000) на оптимальное f с минусом, получим 877192,35 долл. Другими словами, если наша компания захочет инвестировать в маркетинг своего нового продукта в этой отдаленной стране, то в текущий момент оптимальным вложением будет указанная сумма. По мере развития событий в стране сценарии, их исходы и вероятности, скорее всего, будут меняться. Тогда велична f тоже изменится. Чем пристальнее мы будем отслеживать изменение сценариев, чем точнее будут сами эти сценарии, которые мы используем в качестве исходных данных, тем точнее будут наши планы. Заметьте, что если компания не сможет своевременно вложить в маркетинг своего продукта все 877192,35 долл., то она окажется слишком далеко от вершины кривой от f. То же самое можно сказать о трейдере, имеющем слишком много товарных контрактов по сравнению с тем, что диктуется оптимальным f. Если инвестиции пройдут своевременно, но превысят указанную сумму, то это будет аналогично ситуации с товарным трейдером, у которого слишком мало контрактов.
Обращаю ваше внимание на ряд важных обстоятельств, касающихся сценариев и торговли. При формировании сценариев можно использовать массу самых различных факторов:
1. Подобно тому, как это было сделано в предыдущем примере, сценарии можно ассоциировать с исходами данной сделки. Это дает эффект, когда вы торгуете только одним активом. Но если вы торгуете портфелем активов, то вы, скорее всего, нарушаете правило, согласно которому все периоды владения должны иметь одинаковую длину.
2. Если вы знаете, каким будет распределение ценовых исходов, то это можно использовать в сценариях. Предположим, что у вас есть основание полагать, что завтрашнее распределение цен на данный актив будет нормальным. Следовательно, вы можете описывать ваши сценарии на основе нормального распределения. Так, при нормальном распределении в 97,7% случаев прирост цены не превысит двух, а в 99,86% случаев – трех стандартных отклонений. Поэтому один из сценариев может состоять в том, что прирост цены остановится где-то между двумя и тремя стандартными отклонениями (какой бы ни была долларовая величина вашей торговой единицы в течение завтрашнего дня, принимаемого за период владения). Вероятность такого сценария равнялась бы 0,9986-0,9772 = 0,0214, или 2,14%.
3. Вы можете использовать распределения возможных ценовых исходов при торговле одной единицей актива по данной методе в следующем периоде владения. Это мой излюбленный прием, который хорошо согласуется с формированием портфеля по новой методологии.
Хотя я настоятельно рекомендую использовать третий пункт вышеприведенного перечня, какому бы методу вы ни следовали, не забывайте, что по мере изменения условий вам нужно постоянно модернизировать свои сценарии, их исходы и вероятности реализации. Кроме того, следующий период владения нужно открывать, непременно исходя из того, что по формулам является оптимальным в текущий момент. Это аналогично ситуации, в которой находится игрок в очко. С вытягиванием каждой следующей карты комбинация в оставшейся колоде изменяется, как и шансы игрока. Тем не менее, он всегда должен основываться только на текущем раскладе вероятностей.
Хотя обсуждавшиеся выше количественные величины выражались в деньгах, они могут выражаться и в чем-либо другом, – методика остается в силе.
Если вы создаете различные сценарии для рынка акций, то оптимальное f, полученное по этому методу, укажет вам точную долю средств, которую следует вложить на рынке акций в данный момент. Например, если полученное f равно 0,65, это значит, что 65% средств следует вложить в акции, а оставшиеся 35% оставить в наличности. В долгосрочном плане такой подход обеспечит вас наибольшим геометрическим ростом вашего капитала. Разумеется, результат будет не точнее исходных данных, которыми вы снабжаете систему (сценарии, вероятности их реализации, итоговых выплаты и издержки).
Тот же самый процесс можно использовать в качестве альтернативного параметрического метода определения оптимального f для данной сделки. Предположим, что вы основываете свои торговые решения на фундаментальных факторах. При желании вы можете расписать различные сценарии возможных исходов сделки. Чем больше сценариев, чем они точнее, тем лучше будут ваши результаты. Скажем, вы решили заработать на покупке муниципальных облигаций, но не планируете держать их до погашения. Тогда вы можете рассмотреть множество различных сценариев развертывания ситуации в будущем, а затем использовать их при определении того, сколько следует инвестировать в данный конкретный заем.
Предположим, что некий трейдер вынашивает решение о покупке соевых бобов. Он может прибегнуть и к волнам Эллиота, и опереться на прогнозы погоды, но в любом случае он в состоянии определить следующие сценарии этой потенциальной сделки:

Когда наш соевый последователь Эллиота (или трейдер-метеоролог) распишет этот набор сценариев (множество возможных исходов данной сделки) и, стремясь оптимизировать рост своего торгового счета в долгосрочной перспективе, придет к необходимости принятия одного и того же торгового решения в будущем бесконечно много раз, он обнаружит с помощью сценарного планирования, что оптимальным размером позиции в данной сделке будет 0,02 (2%) счета. Это означает открытие одного контракта по соевым бобам на каждые 375000 доллара счета: наибольшая потеря на сценарий, —150 центов за бушель, деленная на оптимальное f = 0,02 для данного набора сценариев, дает 7500/0,02 = 375000 доллара. То есть с одним контрактом на каждые 375000 долл. счета в следующей сделке трейдер будет рисковать 2% своей позиции.
Параметры сценария всякой сделки, безотносительно к тому, чем ее обосновывает трейдер (т. е. волнами Эллиота, погодой и т. д.), могут меняться. Тем не менее, при максимизации геометрического роста своего счета в долгосрочной перспективе трейдер должен исходить из того, что одни и те же параметры сценария будут бесконечно повторяться. Иначе, как мы выяснили на примере рис. 1.2, ему придется серьезно поплатиться. Обратите внимание, что отклонись наш соевый трейдер вправо от вершины f-кривой (взяв немного больше контрактов), он ничего на этом не выиграет. Другими словами, если бы наш соевый трейдер открывал по одному контракту на каждые 300000 долл. счета, то на поверку в долгосрочной перспективе он заработал бы меньше, чем с одним контрактом на каждые 375000 долл.
Если мы имеем дело с принятием решения, каждому аспекту которого соответствует свой набор сценариев, то, выбирая сценарий с наибольшим средним геометрическим при оптимальном f, мы улучшаем наши решения в асимптотическом смысле.
Предположим, что нам нужно принять решение, которое включает два возможных выбора. Их могло бы быть гораздо больше, но для простоты мы ограничимся двумя альтернативами, которые будем называть «белой» и «черной». Если мы выбираем белую альтернативу, то останавливаемся на следующем сценарном раскладе:

Что это за сценарии – неважно. Они могут означать все, что угодно. В дальнейшем обсуждении они будут именоваться по сопоставленным им буквам А, В и С. Неважно также, в чем выражается результат, – это может быть почти все, что угодно.
Пусть, далее, черная альтернатива задается следующим сценарным раскладом:

Многие люди предпочли бы белую альтернативу, поскольку у нее большее математическое ожидание. Выбрав белую альтернативу, вы можете ожидать 3,00 долл. среднего выигрыша на сделку против 2,900 долл. для черной. Однако правильным выбором в действительности является черная альтернатива, поскольку она дает большее среднее геометрическое. Выбрав черную альтернативу, вы можете ожидать 4,53% прибыли (1,0453 – 1) в среднем против 1,23% прибыли для белой. Если учесть эффект реинвестирования, то получим, что черная альтернатива в среднем дает в три с лишним раза больше, чем белая!
Тут читатель может возразить, что «мы не собираемся без конца повторять эту сделку, мы проводим ее лишь однажды. Мы не реинвестируем вновь в одни и те же сценарии. Разве не лучше всегда выбирать сценарий с наибольшим математическим ожиданием для каждого набора решений, с которым мы сталкиваемся?»
Ориентироваться на максимальное арифметическое математическое ожидание нужно лишь тогда, когда вы намерены сделать последнюю ставку и прекратить игру. Однако почти всегда мы продолжаем ее, и деньги, которыми мы рискуем сегодня, завтра же снова будут поставлены на кон. При этом предыдущие выигрыши и проигрыши влияют на то, чем мы в состоянии рискнуть сегодня. В этой ситуации мы заинтересованы в максимальном росте нашего капитала в долгосрочной перспективе и нам следует ориентироваться на большее среднее геометрическое. Даже если сценарии, которые появятся завтра, будут отличаться от сегодняшних, мы все равно максимизируем эффективность наших решений, если всегда будем отдавать предпочтение большему среднему геометрическому. То же самое происходит при выборке без замещения или при игре в очко. От сдачи к сдаче вероятности меняются, как меняется и оптимальная доля счета, которую следует ставить на кон. Однако, постоянно ставя на следующий кон оптимальную долю для текущей сдачи, мы максимизируем наш долгосрочный рост. Помните, что для максимизации долгосрочного роста мы должны исходить из того, что текущий расклад будет бесконечно повторяться в будущем. Другими словами, мы должны рассматривать каждое отдельное событие, как если бы мы ставили на него бесконечное количество раз, если хотим максимизировать рост за много розыгрышей с различными раскладами.
Обобщая, можно утверждать, что если исход события влияет на исход(-ы) следующего события(-ий), то нам лучше предпочесть решение с наибольшим геометрическим ожиданием. В редких случаях, когда исход события не влияет на последующие события, лучше ориентироваться на наибольшее арифметическое ожидание.
Математическое ожидание (арифметическое) не учитывает дисперсии исходов различных сценариев и поэтому может привести к неверным решениям в контексте реинвестирования.
Использование данного подхода к сценарному планированию позволяет выбирать размер позиции, исходя из возможных сценариев, их исходов и вероятностей реализации. Этот подход внутренне более консервативен, чем ориентация на наибольшее математическое ожидание. Среднее геометрическое набора чисел не превосходит их среднего арифметического. Поэтому наш подход никогда не перегрузит (в смысле размера позиции) вас так, как это бывает при ориентации на максимальное математическое ожидание. В асимптотическом смысле (в долгосрочной перспективе) превосходство данного метода проявляется не только в том, что он позволяет вам достичь наибольшего геометрического роста, но также и в большей его консервативности по сравнению с ориентацией на критерий наибольшего математического ожидания.
Поскольку реинвестирование стало чуть ли не каждодневным (за исключением дня, предшествующего уходу от дел), текущие решения нужно принимать, исходя из того, что они будут задействоваться тысячи раз, и таким образом максимизировать их совокупную эффективность. Мы должны принимать свои решения и инвестировать так, чтобы максимизировать геометрическое ожидание. Далее, поскольку исходы большинства событий действительно влияют на исходы последующих событий, мы должны действовать, ориентируясь на максимум геометрического ожидания, что может привести к инвестициям, которые не всегда очевидны.
|