Минимизация ожидаемого среднего общего роста
До сих пор в этой книге, как и в двух ее предшественницах, мы занимались поиском значения f, которое приводило бы к асимптотическому доминированию. То есть для данной рыночной системы мы искали единственное значение f, которое при реальной независимости между сделками с достоверностью приводило бы к максимальному геометрическому росту при стремлении количества сделок (или периодов владения) к бесконечности. Это значит, что в весьма отдаленной перспективе с вероятностью, приближающейся к достоверной, мы выиграли бы больше, чем с помощью любой другой стратегии управления капиталом.
Напомню, что если у нас есть только одна игра, то мы максимизируем рост, прибегая к максимизации среднего арифметического дохода за период владения (т. е. f = 1). Если у нас бесконечное количество игр, то мы максимизируем рост путем максимизации среднего геометрического итога периодов владения (т. е. используем оптимальное f). Однако действительно оптимальное f является функцией планируемой нами продолжительности торговли – количества следующих друг за другом итогов конечных периодов владения (HPR).
Для одного HPR игры с положительным математическим ожиданием оптимальное f всегда будет равно 1,0. Если мы сыграем при любом f, отличном от 1,0, и остановимся после одного периода владения, то мы не максимизируем наш ожидаемый средний геометрический рост. То, что считается оптимальным f, будет таковым, если бы мы сыграли бесконечное количество периодов владения. Для игры с положительным математическим ожиданием действительно оптимальное f начинается с единицы и стремится к оптимальному значению, при стремлении количества периодов владения к бесконечности.
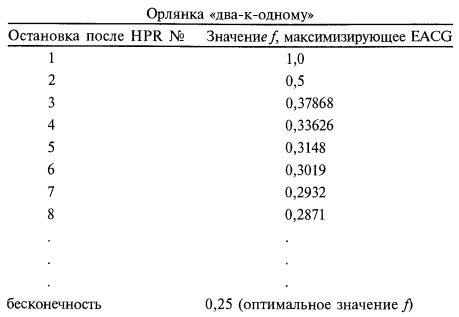
Чтобы убедиться в этом, вновь рассмотрим нашу игру в монетку «два-к-одному», для которой определенное нами оптимальное f равно 0,25. Если в этой игре результат очередного выбрасывания не зависит от предыдущих, то, ставя на каждый кон без пропусков 25% счета, мы наверняка максимизируем наш геометрический рост при стремлении продолжительности игры, или количества подбрасываний (т. е. количества периодов владения), к бесконечности. Это значит, что наш ожидаемый средний геометрический рост, то есть то, чем мы могли бы рассчитывать закончить, – ожидаемая величина по всем возможным комбинациям исходов – будет самым большим, если ставить на кон по 25% счета.


Рассмотрим первое подбрасывание. С вероятностью 50% мы выигрываем два долл. и с вероятностью 50% проигрываем один доллар. Перед вторым выбрасыванием мы имеем следующие шансы: 25% на выигрыш двух долларов при первом выбрасывании и 25% на выигрыш двух долларов при втором; 25% на выигрыш двух долларов при первом выбрасывании и 25% на проигрыш одного доллара при втором; 25% на проигрыш одного доллара при первом выбрасывании и 25% на выигрыш двух долларов при втором; 25% на проигрыш одного доллара при первом выбрасывании и 25% на проигрыш одного доллара при втором (мы считаем эти вероятности истинными, ибо исходим из предпосылки о независимости этих событий – см. раздел «Стохастическая независимость» следующей главы). В ходе игры комбинации образуют древовидную структуру. Поскольку в нашем сценарном спектре только два сценария (орел и решка), из каждого узла игрового дерева отходят только две ветви. Если бы в нашем сценарном спектре было больше сценариев, то и ветвей было бы больше:
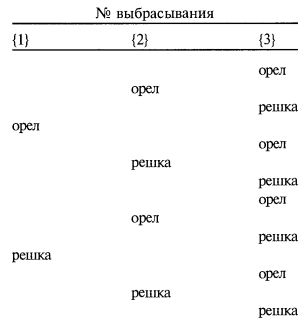
Если мы поставим 25% наших денег на первое выбрасывание и выйдем из игры, то мы не максимизируем наш ожидаемый средний общий рост (EACG).
А что будет, если выйти из игры после второго выбрасывания? Какой тогда должна быть оптимальная ставка, максимизирующая наш ожидаемый средний общий итог, когда в одном случае мы играем при f = 1, и выходим из игры после первого кона, а в другом – играем при оптимальном f и продолжаем игру бесконечно долго?
Если мы вернемся назад и найдем оптимальное f, которое давало бы максимум среднего геометрического HPR за два первых кона в предположении, что при первом и втором выбрасываниях использовались различные значения f, то получим следующее. Во-первых, оптимальное f для выхода из этой игры после двух конов приближается к асимптотически оптимальному, меняя свое значение с 1,0 (выход после первого кона) на 0,5 для первого и второго кона. То есть если бы мы собирались выйти из игры после второго кона, то для максимизации роста нам следовало бы на оба кона, первый и второй, ставить по 0,5 счета. Напоминаю, что мы имеем право для первого и второго кона брать разные значения f. Но в данном случае они оказываются одинаковыми: 0,5. Дело в том, что максимум роста для конечных и бесконечных потоков достигается на одном и том же оптимальном f.
Мы можем убедиться в этом, если рассмотрим две первых возможных комбинации выбрасываний монеты:

Откуда, перейдя к исходам, получаем:

Эти исходы можно преобразовать в итоги периодов владения
для различных значений f. Ниже это сделано для f = 0,5, как при первом, так и при втором выбрасывании монеты:

Теперь мы можем выразить все выбрасывания, следующие за первым, в виде значений TWR с помощью умножения на последующие выбрасывания согласно дереву игры. Число в скобках, стоящее рядом с последней ветвью дерева – это корень степени п из последнего значения TWR (n равно количеству HPR, или выбрасываний, в данном случае – 2), который является средним геометрическим HPR для конечного узла дерева:

Если теперь сложить средние геометрические значения HPR и взять арифметическое среднее, то получим ожидаемый средний общий доход. В данном случае он будет равен:
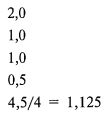
Следовательно, если бы мы прекращали игру после двух конов, но делали бы это бесконечное количество раз (т. е. останавливались после двух конов), ставя на каждый кон без пропусков оптимальные 50% счета, то максимизировали бы тем самым наше EACG.
Обратите внимание, что ставка первого кона не соответствовала f = 1,0, хотя это оптимизировало бы ожидаемый средний общий рост, остановись мы после этого. Вместо этого, планируя остановиться после двух конов, мы максимизируем EACG, ставя на оба кона по 0,5 счета.
Заметьте, что оптимальное f, доставляющее максимум роста, одинаково для всех конов игры, хотя и является функцией того, как долго вы будете играть. Если вы собираетесь остановиться после первого кона, то оптимальное f максимизирует среднее арифметическое HPR (для игры с положительным математическим ожиданием это f всегда равно 1,0, а игры с отрицательным математическим ожиданием – 0,0). Для игры с положительным математическим ожиданием оптимальное f убывает по мере увеличения времени до остановки (асимптотически убывает для бесконечной игры) и максимизирует среднее геометрическое HPR. Для игры с отрицательным математическим ожиданием оптимальное f всегда остается нулевым.
Однако в течение всей игры значение f, которое вы используете для максимизации роста, остается постоянным, и эта постоянная величина зависит (функционально) от того, где вы собираетесь прекратить игру. Если вы играете в орлянку «два-к-одному» и собираетесь остановиться после первого кона, то получите максимальный рост при f = 1,0. Если вы собираетесь остановиться, сыграв два кона, то получите максимальный рост при f = 0,5, как при первом, так и при втором выбрасывании. Заметьте, что, желая максимизировать EACG для остановки после второго кона, вы не ставите все свои деньги (1,0 счета) на первый кон. Аналогичным образом, планируя играть бесконечно долго, вы и на первый, и на все следующие выбрасывания будете ставить по 0,25 счета.
Обращаю ваше внимание на радикальное отличие понятий бесконечно и неограниченно. Все потоки конечны, всем нам суждено в конце концов умереть. Поэтому, когда мы говорим, что оптимальное f максимизирует ожидаемый средний общий итог, то имеем в виду такое f, которое максимизирует его при бесконечной игре. На деле, оно слегка отличается от оптимального, ибо никто из нас не сможет играть бесконечно долго. То f, которое даст максимум EACG, будет немного больше того, что мы называем оптимальным f, а наши позиции – немного крупнее.
А что получится, если мы остановимся, сыграв три кона? Должно ли тогда f, которое максимизирует ожидаемый средний общий рост, быть меньше 0,5 (остановка после двух конов), но все же больше оптимального f = 0,25 для бесконечной игры?
В этом случае наше дерево комбинаций будет следующим:
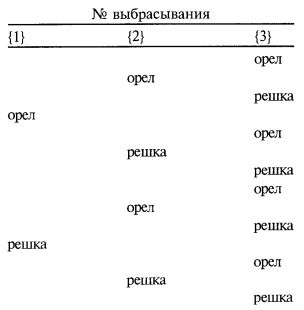
Преобразуя это дерево в исходы, получим:

Если мы обратимся к компьютеру и путем перебора найдем значение f, которое максимизирует средний общий рост при остановке после трех розыгрышей, то получим f = 0,37868. Преобразуя исходы в HPR при данном значении f, получим:

Теперь мы можем выразить все выбрасывания, следующие за первым, в виде значений TWR с помощью умножения на последующие выбрасывания согласно дереву игры. Число в скобках, стоящее рядом с последним выбрасыванием дерева, – это корень степени п из последнего значения TWR (я равно количеству HPR, или выбрасываний, в данном случае – 2), который является средним геометрическим HPR для конечного узла дерева:
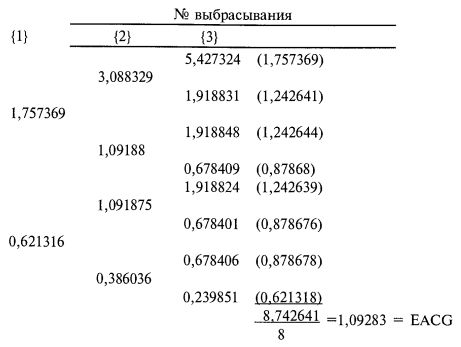
Если вы хоть чуть сомневаетесь в полученных результатах, то я рекомендую вам перепроверить несколько последних выкладок с карандашом и бумагой или на компьютере и найти значения f, которые дадут EACG, больше представленного. Допустите возможность использования разных f, то есть, что f может меняться при каждом выбрасывании. Вы обнаружите, что ваши результаты совпадают с нашими и что величина f постоянна, хотя и зависит от длины игры.
Подводя итоги, приходим к следующим выводам:
1. Максимизируя ожидаемый средний общий рост (EACG), мы всегда приходим к постоянной величине f. То есть величина f не меняется от кона к кону.
2. То f, которое оптимально в смысле максимизации EACG, является функцией от длины игры. Для игр с положительным математическим ожиданием оно изменяется от 1,0, максимизирующего среднее арифметическое HPR, немного уменьшаясь с каждым коном, и асимптотически приближается к такому значению, которое максимизирует среднее геометрическое HPR (это значение мы будем далее называть оптимальным f).
3. Поскольку длина всякого потока конечна, то наша торговля на основе оптимального f всегда будет слегка субоптимальной, независимо от того, как долго мы торгуем. Однако различие с каждым периодом владения будет уменьшаться. В итоге мы окажемся слева от вершины, положение на которой действительно оптимально. Это ни в коей мере не отрицает всего сказанного об (n + 1)-мерного изображения в пространстве рычагов (недостатки и преимущества положения рыночной системы относительно своего оптимального f). Но само это изображение зависит от количества периодов владения, на котором мы останавливаемся. По мере удлинения игры она асимптотически приближается к действительно оптимальной поверхности, которую мы выстраиваем с помощью приемов, излагаемых в книге.
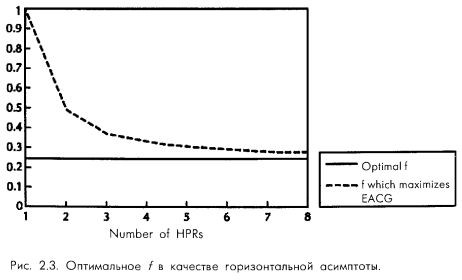
Чтобы убедиться в сказанном, продолжим нашу орлянку «два-к-одному». На графике (рис. 2.3) показаны значения f, которые максимизируют наш ожидаемый средний общий рост при остановке после 1-8 конов. Обратите внимание, что они приближается к оптимальному значению 0,25, которое асимптотически максимизирует рост при стремлении количества периодов владения к бесконечности.
В реальности, если мы торгуем при значении f, которое в этой книге называется оптимальным, тем не менее, мы останемся немного субоптимальны, и степень этой субоптимальности будет уменьшаться по мере того, как будет проходить все больше и больше периодов владения. Если бы мы точно знали, сколько периодов владения будем торговать, то могли бы использовать то значение f, которое максимизирует EACG и действительно оптимально для этого количества владений (оно было бы несколько больше оптимального f). К сожалению, мы редко с определенностью можем сказать, сколько периодов владения будем торговать, поэтому остается утешаться тем фактом, что оптимальное f приближается к оптимальному значению для максимизации EACG по мере истечения все большего количества периодов владения. В заключительной главе этой книги мы познакомимся с методами постоянного доминирования, которые позволят нам подойти к идее максимизации EACG в условиях разделения счета на активную и пассивную части (т. е. когда торговля ведется менее агрессивно, чем это рекомендуется оптимальным f).
Обратите внимание, что ни одна из этих идей не рассматривается или даже не упоминается в старых среднедисперсионных моделях по типу «риск-прибыль». Старые модели почти полностью игнорируют фактор финансового рычага и последствия его применения, что еще раз указывает на предпочтительность нашего нового подхода.
|