Свойства функций полезности
Функции полезности имеют пять основных свойств:
1. Функции полезности инвариантны относительно положительных линейных преобразований. Так, функция предпочтения полезности ln х, приведет к выбору тех же инвестиций, что и функции полезности 25 + ln х, 7 * ln x или (ln х)/1,453456. То есть функция полезности, подвергнутая воздействию положительной константы (прибавлением, вычитанием, умножением или делением), приведет к выбору тех же самых инвестиций. Другими словами, она приведет к тому же набору инвестиций, максимизирующих полезность, что и до воздействия на нее положительной константой.
2. Большее предпочтительнее меньшего. В экономической литературе это часто называется ненасыщением. Другими словами, функция полезности никогда не приведет к предпочтению меньшего капитала большему при достоверных исходах или равенстве их вероятностей. Поскольку при росте капитала должна расти и полезность, то первая производная от полезности как функции капитала должна быть положительной. То есть:

Если полезность измерять по вертикальной оси, а капитал – по горизонтальной, то у кривой полезности никогда не будет отрицательного наклона.
Первой производной функции полезности ln x будет х-1.


3. Предполагается три возможных типа отношения инвестора к риску, называемых также нерасположенностью к риску.
Он может либо уклоняться от риска, либо быть нейтральным к нему, либо жаждать риска. Все эти категории могут
быть описаны в терминах справедливой азартной игры. Если
взять справедливую игру, такую, как подкидывание монеты, с выигрышем одного доллара на орлах и проигрышем одного доллара на решках, то мы обнаружим, что математическое ожидание капитала равно нулю. Уклоняющийся от риска индивидуум отверг бы такое пари, тогда как жаждущий риска его бы принял. Инвестор, который нейтрален к риску, был бы индифферентен к этому пари.
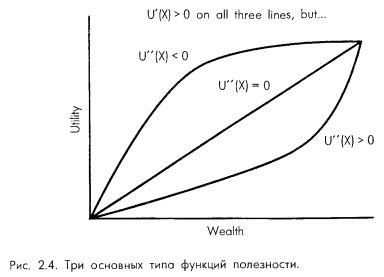
Неприятие риска характеризуется второй производной функции предпочтения полезности U"(x). У индивидуума, уклоняющегося от риска, вторая производная отрицательна, у склонного к риску – положительна, а у нейтрального к риску – вторая производная функции предпочтения риска нулевая.
На рис. 2.4 изображены три основных типа функций предпочтения полезности в зависимости от U"(x), или степени неприятия риска инвестора. Функция предпочтения полезности, равная ln х, демонстрирует нейтральное отношение к риску. Инвестор индифферентен к справедливой азартной игре. Для логарифмической функции предпочтения полезности вторая производная будет равна –х-2.
4. Четвертое свойство функций предпочтения полезности касается того, как изменяется степень неприятия риска инвестора при изменении капитала. При этом говорят об абсолютной величине нерасположенности к риску. Здесь вновь имеются три категории. К первой относятся индивидуумы, которые проявляют возрастающее абсолютное неприятие риска. По мере роста капитала они держат все меньше средств в рискованных активах. Следующими идут индивидуумы с постоянным абсолютным неприятием риска. С ростом капитала они сохраняют те же денежные вложения в рискованные активы. Последними идут те, кому свойственно понижение абсолютного неприятия риска. С ростом капитала они готовы держать больше денег в рискованных активах.
Математически абсолютное неприятие риска А(х) выражается следующим образом:

Если нам нужно узнать, как изменяется абсолютное неприятие риска с изменением капитала, то мы берем первую производную от А(х) по х (капитал) – А'(х). При этом у индивидуума с возрастающим абсолютным неприятием риска было бы А'(х) > 0, при постоянном абсолютном неприятии риска было бы А'(х) = 0, а при понижающемся абсолютном неприятии риска было бы А'(х) < 0.
В случае логарифмической функции предпочтения полезности имеет место понижающееся абсолютное неприятие риска. Для ln х имеем:
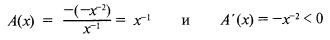
5. Пятое свойство функций предпочтения полезности касается того, как изменяется доля средств, инвестированных в рискованные активы, с изменением капитала. При этом говорят об относительной величине нерасположенности к риску. Другими словами, это касается того, как изменяется доля, а не денежная величина средств, инвестированных в рискованные активы, в зависимости от изменения капитала. Здесь вновь имеются три возможные категории: возрастающее, постоянное и убывающее относительное неприятие риска, где доля инвестиций в рискованные активы возрастает, постоянна или убывает, соответственно.
Математически относительное неприятие риска R(x) выражается следующим образом:
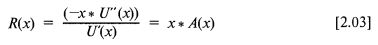
Отсюда R'(х), первая производная относительного избегания риска, будет характеризовать, как изменяется относительное неприятие риска в зависимости от изменений капитала. Поэтому индивидуумам, которым свойственно возрастание, постоянство и понижение относительного неприятия риска, будут отвечать положительная, нулевая и отрицательная R'(х), соответственно.
В случае логарифмической функции предпочтения полезности имеет место постоянное относительное неприятие риска. Для ln х имеем:

|