Количество реализаций (частота) и вероятность
Чаще всего совместные вероятности для двух случайных переменных представляются в табличной форме. Например, для нашего потока исходов одновременного бросания двух монет (OO, ОР, РО, РР) мы можем составить таблицу, демонстрирующую эти четыре одновременных события:

Часто с помощью таблиц представляют и вероятности:
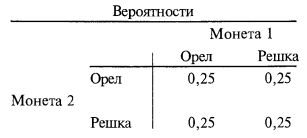
Мы предполагаем, и вполне правомерно, что между двумя монетами нет никакой корреляции. То есть исходы бросаний двух монет не зависят друг от друга. Если бы это было не так, то каждый из четырех возможных исходов (ОО, ОР, РО, РР) не имел бы одну и ту же вероятность реализации.
Теперь введем понятие стохастической независимости. Если совместная вероятность двух событий равна произведению их индивидуальных вероятностей (как в нашем примере с бросанием монеты), то говорят, что налицо стохастическая независимость. То есть, когда верно выражение

тогда имеет место стохастическая независимость. Часто через это уравнение определяют совместную вероятность независимых случайных переменных.
Стохастическая независимость, следовательно, синонимична в используемом нами смысле нулевому коэффициенту корреляции между двумя потоками исходов.


Поэтому при наличии стохастической независимости мы можем говорить, что коэффициент корреляции равен нулю. Обратное, однако, неверно. Мы вскоре увидим, что бывает и так, когда коэффициент корреляции равен нулю, а стохастической независимости нет.
Когда мы говорим о таблице исходов одной случайной переменной, мы имеем в виду безусловное распределение этой переменной. Например:

Когда речь идет о таблице исходов большего количества переменных, мы имеем в виду то, что называется совместным распределением переменных. Например:

Обычно условные вероятности рассматриваются в предположении стохастической независимости. Во многих случаях, вроде бросания двух монет, это предположение оправданно. Но есть масса реальных ситуаций, например, при оценке вероятности того, что в определенный день одновременно вырастут две акции (акции обычно положительно коррелированны друг с другом, т. е. коэффициент корреляции > 0), это традиционное предположение теряет силу. Совместные вероятности нельзя рассчитать простым перемножением индивидуальных вероятностей.
Эта проблема изводила меня в течение трех лет. Я пытался найти решение на пути обобщения теории условных вероятностей. То есть такое, которое бы давало условные вероятности для любых значений коэффициента корреляции, а не только для удобных значений, вроде 0, 1 или –1. Мне нужна была теория, которая давала бы условные вероятности для всех значений коэффициента корреляции между двумя случайными переменными.
Я докучал университетам, докторам математики, свихнувшимся профессорам, южноамериканским знахарям, статистикам из страховых обществ и всем прочим, кто, по моему мнению, мог бы иметь ключ к этой проблеме. Часами я просеивал горы скучных технических журналов.
Я лично непрестанно искал решение этой проблемы. Я безрезультатно возился с идеей суперпозиции двух распределений исходов под углом между ними, согласно коэффициенту корреляции, вычисляя интегралы по образуемым ими поверхностям. Долгое время я думал, что смогу воспользоваться направляющими (частью очевидных на желаемых вероятностях и туманных в остальном). Я хотел выстроить их под углами, согласно их корреляции, пустить вектора, которые пройдут через очевидные части. Пересекаемые ими области будут разделены параллелограммом, образованным возможными зонами пересечения событий, откуда будут получены совместные вероятности. Я вывел все необходимые формулы и запрограммировал их в виде огромных электронных таблиц для анализа результатов этой концептуальной эквилибристики. На это ушла масса блокнотных страниц, салфеток и этикеток спичечных коробков.
Чем больше я работал над этой проблемой, тем более важным казалось мне ее решение. Почему же никто не мог решить проблему совместных вероятностей, столь важной для практических нужд? Почему же условные вероятности проработаны лишь для самых удобных значений коэффициента корреляции? Это было единственное, чего не хватало нашей новой методологии инвестирования. Я вывел целевую функцию, но в ней в качестве аргументов использовались именно эти условные вероятности.
Как вы увидите в следующей главе, для реализации более совершенного подхода к инвестированию имелось все, кроме способа расчета совместных вероятностей по любым значениям коэффициента корреляции между двумя потоками случайных переменных.
Подлинное страдание причиняла мне известная теорема об условных вероятностях, утверждавшая, что совместную плотность вероятности нельзя получить из безусловных плотностей вероятности компонент. Согласно традиционной точке зрения считалось, что в отсутствие стохастической независимости функция совместной плотности вероятности является уникальной, вполне самостоятельной, которая возникает как бы ниоткуда! То есть она не выражается через функции безусловных плотностей составляющих, а есть новая, самостоятельная функция плотности вероятности, которая не может быть восстановлена из функций безусловных плотностей составляющих. Чтобы убедиться в этом, рассмотрим следующую таблицу, позаимствованную у Феллера, которую мы графически проиллюстрировали на рис. 3.1.
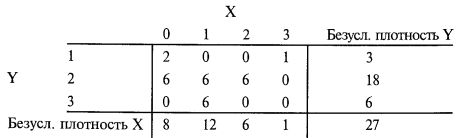
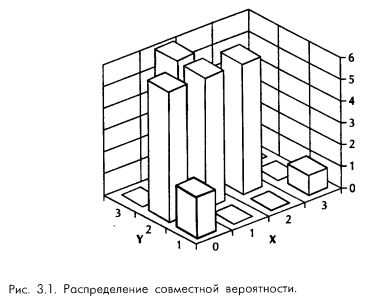
Коэффициент корреляции между потоками исходов события X и события Y равен нулю. Поэтому, если бы имела место стохастическая независимость, то можно было бы ожидать, что вероятность Х = 0 и Y = 3 будет равна (6/27) * (8/27) = 0,222 * 0,0658 = 0,0658. Вместо этого, эта вероятность равняется нулю, подтверждая тем самым принятую теорему условных вероятностей о том, что совместные плотности не могут быть получены из безусловных плотностей компонентов.
Было известно, как определять коэффициент корреляции при наличии только совместной плотности и безусловных плотностей, но долгое время считалось, что нельзя определить совместную плотность, располагая лишь безусловными плотностями и коэффициентом корреляции потоков. А именно это мне и было нужно.
Я не мог принять традиционную точку зрения и стал еще более одержим поисками такого решения этой проблемы, которое было бы четким и легко применимым на практике. То есть мне нужно было такое решение, посредством которого при наличии коэффициента корреляции и вероятностей, ассоциированных с двумя сценарными спектрами (например к двум монетам, имеющими два равновероятных сценария О и Р), представленными двумя безусловными плотностями вероятности, можно было бы рассчитать плотность совместной вероятности.
В конце концов я понял механизм формирования совместной плотности вероятности из безусловных плотностей вероятности. Однако, как вы увидите, этот механизм оказался не столь четким и простым, как мне бы хотелось.
Природа вновь не идет на сотрудничество.
Рассмотрим два одновременных сценарных спектра с ненулевым коэффициентом корреляции и оценим вероятность совместной реализации двух заданных сценариев, по одному из каждого спектра.
Вспомним, что, когда мы бросаем две монеты и исходы стохастически независимы (т. е. коэффициент линейной корреляции r равен 0), вероятность выпадения двух орлов равна произведению индивидуальных вероятностей (см. формулу [3.01]):
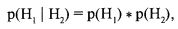
или в более краткой форме:
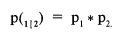
Теперь давайте представим себе, что две наши монеты могут телепатически общаться между собой так, что, когда первая монета выпадает орлом, вторая также выпадает орлом. Это ситуация соответствует коэффициенту линейной корреляции r, равному 1. Вероятность выпадения двух орлов равна 0,5 – вероятности выпадения орла на первой монете.
Если бы коэффициент корреляции был равен –1 (то есть если первая монета выпадает орлом, то вторая обязательно – решкой), то при бросании двух монет вероятность выпадения двух орлов была бы равна нулю. Однако вероятность выпадения на первой монете орла, а на второй монете – решки равна 0,5, что равно вероятности выпадения на первой монете орла (так как r = –1, вторая монета всегда выпадает решкой, если первая выпала орлом).
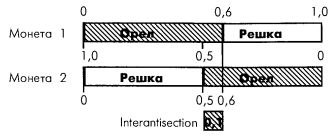
Введем теперь понятие, которое за неимением лучшего термина будем называть интерантисечением. Для этого вновь обратимся к случаю r = 1, то есть, когда при выпадении одной монеты орлом, другая монета также выпадает орлом. Мы говорим, что вероятность этого (0,5) равна вероятности выпадения одной из монет орлом, поскольку используются идеальные монеты с вероятностью выпадения орла, равной 0,5.

Предположим далее, что одна из монет не идеальна и вероятность выпадения на ней орла равна не 0,5, а 0,4. Теперь вероятность выпадения двух орлов будет равна 0,4 – меньшая из вероятностей перекрывает большую.
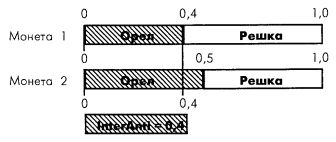
Если бы вероятность выпадения решки была равна 0,4 (и, следовательно, вероятность выпадения орлов была бы равна 0,6), то вероятность выпадения двух орлов была бы равна 0,5 – меньшей из двух вероятностей (так как вероятность орла на одной монете равна 0,6, а на другой равна 0,5).
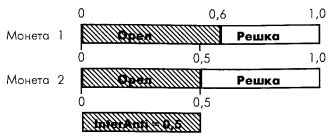
При этом у какой из монет, первой или второй, вероятность меньше, роли не играет:

Интерантисечение при r = 1 и есть описанное перекрытие, то есть меньшая из двух вероятностей. На предыдущем рисунке интерантисечением выпадения обеих монет решкой будет 0,4. Другими словами, при положительном r интерантисечение есть пересечение двух вероятностей.
Когда коэффициент корреляции отрицателен, второй сценарный спектр (в данном случае монета 2) переворачивается на 180 градусов.
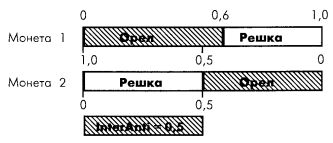
Заметьте, что на предыдущем рисунке вторая монета переворачивается на 180 градусов, давая тем самым совместную вероятность 0,5 выпадения орла на первой монете (с вероятностью 0,6) и решки (с вероятностью 0,5) – на второй, если коэффициент корреляции между двумя монетами равен – 1.
Если бы мы захотели найти интерантисечение выпадения двух орлов, то, как явствует из следующего рисунка, получили бы вероятность 0,1.
Вспомните теперь, что при бросании двух монет в условиях стохастической независимости между ними (т. е. коэффициент линейной корреляции r = 0), вероятность выпадения двух орлов равнялась произведению индивидуальных вероятностей (см. уравнение [3.01]):
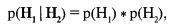
или в более краткой форме:
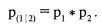
Следовательно, для идеальных монет (т. е. у каждой вероятность выпадения орла равна 0,5) при нулевом коэффициенте вероятность выпадения двух орлов будет равна:
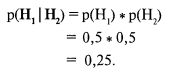
Но когда коэффициент корреляции равен 1, совместная вероятность представляет собой пересечение индивидуальных вероятностей, или 0,5 в данном случае. Когда коэффициент корреляции равен –1, это будет пересечение после поворота на 180 градусов (антисечение) одного из сценарных спектров, что в данном случае даст нулевую вероятность выпадения двух орлов.
Итак, мы научились находить совместные вероятности, когда коэффициент корреляции между двумя сценарными спектрами равен –1 или 1. Как же нам аппроксимировать совместные вероятности, когда коэффициент корреляции имеет не столь удобные значения?
Обратите внимание на два фактора, которые влияют на совместные вероятности. Первый из них – это произведение индивидуальных вероятностей (при r = 0):
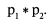
Вторым из них является интерантисечение двух вероятностей (при |r| = 1):
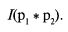
Нижним пределом совместных вероятностей является нуль, получающийся, когда интерантисечение равно 0, а также, когда хотя бы одна из вероятностей P1 или р2 равна 0. Тогда и первый фактор, произведение двух вероятностей, и второй фактор, их интерантисечение, будут нулевыми.
Верхний предел величины совместной вероятности может быть меньше меньшего из P1 или р2. В этом легко убедиться, ибо фактор интерантисечения никогда не может быть больше, чем минимум из P1 и р2. Поскольку вероятность не может быть больше 1, то произведение P1 * p2 не может быть больше меньшего из P1 и р2. То есть мы можем утверждать, что верхний предел величины совместной вероятности равен меньшей из вероятностей.
Исходя из нулевой нижней границы и верхней границы, равной минимуму из P1 и р2, будем искать условную вероятность в виде линейно взвешенной суммы двух этих факторов:
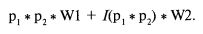
Но что мы будем использовать в качестве весов W1 и W2? Как оказывается, W1 равен 1 минус абсолютная величина коэффициента корреляции:
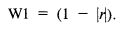
A W2 есть просто абсолютная величина коэффициента корреляции:
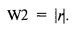
Эта весовая схема гарантирует нам, что мы останемся в пределах верхних и нижних границ. Так, когда r = 0, наше уравнение целиком склоняется в пользу произведения двух вероятностей, а когда |r| = 1, перевес будет целиком в пользу интерантисечения. Полностью уравнение для аппроксимации совместных вероятностей имеет вид:
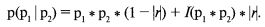
Мы называем функцию линейно взвешенной (т. е. ни один из ее аргументов не имеет степени большей единицы), так как ее графиком служит прямая линия. Мы можем убедиться в линейности соотношений между p1 * р2 и I(p1 * p1), наблюдая за следующими двумя потоками исходов бросания монеты:
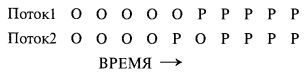
Если приглядеться к этим двум потокам, то мы увидим, что в каждом из них вероятность исхода О и исхода Р равна 0,5. Подсчитав коэффициент корреляции между этими потоками, получим 0,6.
Далее, для r = 0 получаем P1 * р2 = 0,5 * 0,5 = 0,25. Если нас интересует выпадение орлов в обоих потоках одновременно, то получаем интерантисечение I(P1 * p2), равное 0,5:
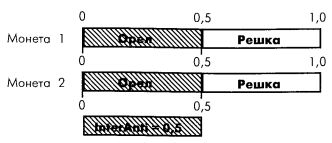
Если коэффициент корреляции больше 0, то мы не разворачиваем сценарный спектр на 180 градусов. Заметьте, что, когда нас интересует интерантисечение обоих потоков, одновременно дающих решку, получим, что его величина также равна 0,5.
При r = 0 имеем, что совместная вероятность выпадения обоих орлов равна p1 * p2 (или, как в данном случае, и для обеих решек). При r = 1 имеем совместную вероятность, равную интерантисечению 0,5. При r = –1 интерантисечение было бы равно 0, а, значит, и совместная вероятность равна 0, как явствует из следующего рисунка.

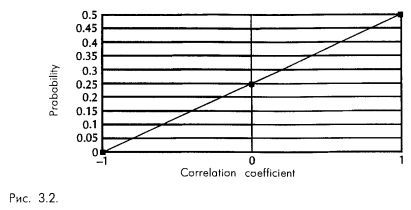
Таким образом, получаем следующие три точки, в которых мы уверены:

Изобразим эти три точки на графике (см. рис. 3.2.).
Мы видим, что эти три точки можно соединить прямой линией. Впрочем, их можно соединить и какой-нибудь кривой (т. е. функция не будет линейно взвешенной), например сигмоидой (т. е. растянутой S-образной кривой, проходящей через наши три точки).
Итак, в обоих потоках орел выпал четыре раза из десяти (аналогично, решка выпала в обоих потоках четыре раза из десяти), что дает вероятность 0,4. Обратите внимание, что если функция линейна, то есть изображается на графике прямой линией, то эта прямая проходит через точку, соответствующую коэффициенту корреляции 0,6 и вероятности 0,4. Если бы график функции отличался от прямой, то коэффициенту корреляции 0,6 соответствовало бы все, что угодно, кроме 0,4! (см. рис. 3.3).
Теперь рассмотрим нашу функцию применительно к этим двух потокам исходов:
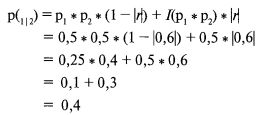
То есть мы видим, что наша формула дает такой результат, который подтверждается самим потоком исходов. Мы можем ожидать появления орлов в обоих потоках одновременно с вероятностью 0,4, при бросании двух идеальных монет с коэффициентом корреляции r = 0,6.
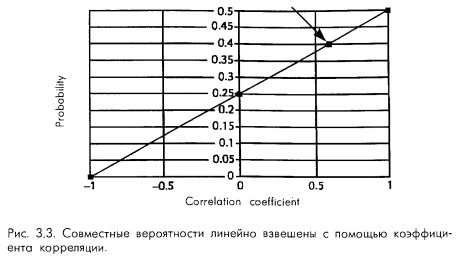
Эта аппроксимация проходит только в случае биномиального распределения (т. е. при двух сценариях в спектре). Чем более уклоняются вероятности от 0,5 на сценарий, тем менее точной она становится. Другими словами, это решение является точным, когда вы дихотомизируете два сценарных спектра; в противном случае она превращается в аппроксимацию убывающей точности.
Впрочем, любые сценарные спектры можно свести к биномиальным распределениям (наборам только из двух сценариев), путем дихотомизации около их центров. Вновь обратимся к сценарному спектру нашей промышленной компании. Он содержит восемь различных сценариев. Мы можем дихотомизировать их, объединив воедино сценарии Войны, Кризиса и Стагнации в один сценарий нового сценарного спектра, который мы будем называть сценарием Плохой половины исходов. Аналогичным образом, мы можем объединить воедино сценарии мира и процветания в сценарий Хорошей половины исходов нового спектра. Теперь мы можем обращаться с преобразованным спектром так же, как и с другими спектрами, содержащими по два сценария, и аппроксимировать совместные вероятности четырех возможных совместных исходов (рис. 3.4).
Дихотомизация сценарных спектров для аппроксимации совместных вероятностей эффективна лишь до тех пор, пока вы разделяете их примерно на равновероятном уровне (0,5). Чем дальше от него проводится дихотомизация, тем менее точной становится аппроксимация.
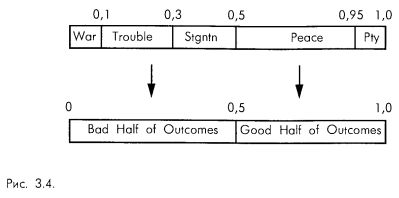
Вновь обратимся к примеру из Феллера, приведенного в начале этой главы:
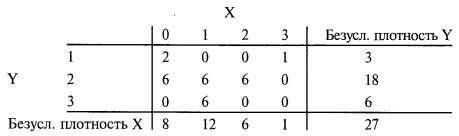
Если дихотомизировать сценарный спектр X, объединив исходы 0 и 1 в сценарий А спектра X, а исходы 2 и 3 в сценарий В спектра X, то мы удалимся от равновероятного уровня. Уровень, который мы получим при такой дихотомизации, будет равен 0,74074, поскольку, судя по безусловным плотностям в X, двадцать из двадцати семи исходов (74,074%) приходятся на 0 или 1, и только семь из двадцати семи исходов (25,92%) приходятся на 2 или 3 (см. рис. 3.5).
Если то же самое проделать со сценарным спектром Y, объединяя исходы 1 и 2 в сценарий А спектра Y, а исход 3 переименовывая в сценарий В спектра Y, то преобразованный спектр Y станет таким, как показано на рис. 3.6.
Заметьте, что спектр Y также дихотомизирован не равновероятно, а поблизости к 0,777.
Приступим к формированию таблицы совместных вероятностей в следующем виде:
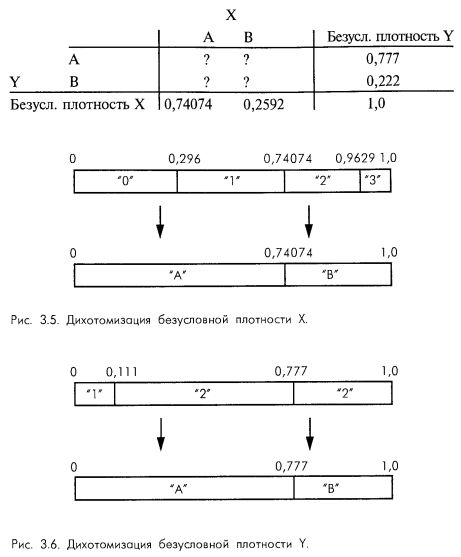
Теперь, исходя из того, что коэффициент корреляции r между этими двумя сценарными спектрами равен 0, определим четыре совместные вероятности нашей таблицы:
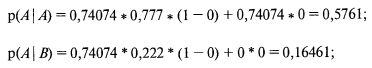
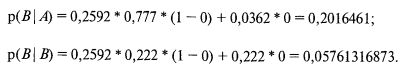
(Обратите внимание на величины интерантисечений в предыдущих уравнениях.)
Теперь мы можем завершить таблицу:
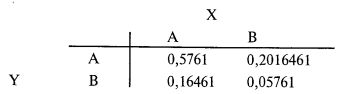
Поскольку в исходной таблице мы использовали не вероятности, а фактические замеры по двадцати семи реализациям, мы можем умножить полученные вероятности на двадцать семь и получить таблицу ожидаемых частот:
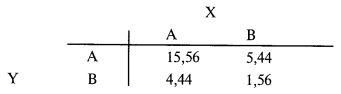
Мы видим, что можно ожидать 15,56 реализаций (из двадцати семи) по сценарию А из спектра X и по сценарию А из спектра Y. Вспомните, что это соответствует реализации 0 или 1 исходного спектра X и 1 или 2 исходного спектра Y. Переходя к исходному спектру, обнаруживаем, что на самом деле таких реализаций было четырнадцать (из двадцати семи):
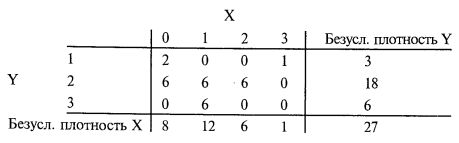
Сходные ошибки можно найти и в других трех квадрантах. Такой неточностью мы обязаны тому, что дихотомизировали исходное распределение слишком далеко от действительно равновероятного уровня (мы дихотомизировали на уровнях 0,74074 и 0,777). Поэтому наши аппроксимации совместных распределений оказались менее точными.
Давайте вернемся назад и дихотомизируем эту таблицу на уровнях 0,5. Для этого попытаемся ответить на вопрос: «Где на оси X находится уровень 0,5?»
Сначала просуммируем произведения каждого исхода X на его частоту:

Теперь разделим полученную сумму на общее количество реализаций (27) и найдем взвешенное по вероятности среднее:
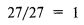
Это значит, что если бы это было непрерывное распределение, то мы могли бы ожидать 50% реализаций меньше 1 и 50% – больше.
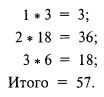
Теперь разделим полученную сумму на общее количество реализаций (27) и найдем взвешенное по вероятности среднее:
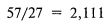
То есть если бы это было непрерывное распределение, то мы могли бы ожидать 50% его реализаций меньше 2,111 и 50% – больше.
Теперь рассчитаем вероятности для четырех квадрантов:
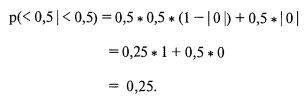
«Подождите, – скажете вы, – поскольку имеет место стохастическая независимость, нет нужды все это проделывать; мы можем просто перемножить вероятности для каждого из четырех квадрантов и определить вероятности, ассоциированные с каждым квадрантом. Это даст совместную вероятность 0,25 для каждого квадранта» Все это совершенно верно. Квадранты разделены точно значением 1 по X и значением 2,111 по Y. То есть в каждом квадранте мы можем ожидать 25% всех реализаций, или 6,75 реализаций из 27 (27 * 0,25).
Глядя на таблицу, может оказаться сложновато выделить в каждом квадранте 6,75 исходов: ведь в ней представлены дискретные исходы, а мы для удобства дихотомизации таблицы на равновероятных уровнях обращались с ними, как с непрерывными. Например, если взять строку реализаций Y для исхода «2», то сколько их будет ниже, а сколько выше уровня 2,111?
Разумеется, в случае более удобных распределений механизм образования совместных вероятностей из составляющих безусловных вероятностей более нагляден.
А сейчас рассмотрим другую ситуацию с двумя потоками исходов двенадцати конов:

Мы можем определить, что коэффициент корреляции этих двух потоков равен 0,33333. Если мы теперь примемся составлять таблицу совместных вероятностей, то определим также и безусловные плотности (каждый из четырех сценариев каждого сценарного спектра имеет вероятность реализации 0,25).

Если мы теперь проведем дихотомизацию точно на уровне 0,5 для обоих сценарных спектров, то в каждом спектре получим по два сценария, которые будем называть «+» и «–». Вероятность реализации каждого сценария в спектре равна 0,5. Сценарий «+» включает те исходы, которые больше 0, а сценарий «–» содержит исходы, меньшие 0. Таблица будет выглядеть следующим образом:
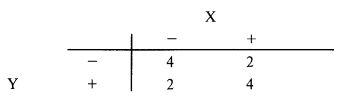
Вернемся теперь к нашему уравнению для определения совместных вероятностей и посмотрим, насколько близки эти данные к расчетным:


Таким образом, наша формула дает следующие оценки совместных вероятностей:

Если умножить их на количество исходов (12), то получим следующую таблицу частот ожидаемых исходов:
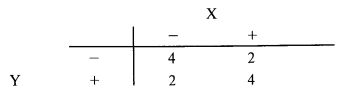
Это точно совпадает с эмпирическими данными потока исходов. Заметьте, что такая точность объясняется тем, что мы провели дихотомизацию на уровне 0,5.
Судя по таблице, мы, например, можем ожидать отрицательного числа в потоке X и отрицательного числа в потоке Y в четырех из двенадцати случаев и так далее (для трех других квадрантов.
«Подождите, – скажете вы, – разве нельзя взять один из этих квадрантов и дихотомизировать его для получения более детальных вероятностей, не ограничиваясь достигнутым?» Другими словами, в этом примере вы хотите знать не только, какова вероятность, скажем, положительного числа в обоих потоках, но и какова вероятность –2 в потоке X и –1 в потоке Y. То, чему мы пока что научились, даст вам точное совместное распределение, если у вас есть два бинарных безусловных распределения – то есть, когда у вас есть два безусловных распределения, каждое из которых имеет только два возможных исхода, два возможных сценария (как в большинстве азартных игр, где вы выигрываете М с вероятностью Х и проигрываете N c вероятностью Y). Однако хотелось бы получать совместные распределения для любых безусловных распределений, а не только для бинарных.
Тут-то мы и подходим к сути дела.
|