Активный и неактивный капитал
Когда мы торгуем оптимальным портфелем по всему капиталу, мы можем ожидать ужасных текущих потерь по всему портфелю в смысле сокращения собственных средств на счете.
Наша единственная защита от этого – каким-то образом разбавить портфель. Степень риска и безопасности любой инвестиции, следовательно, не есть функция самой этой инвестиции, а, скорее, функция уровня такой разбавленности.
Даже портфель из акций голубых фишек, когда они торгуются на их оптимальных геометрических уровнях, продемонстрирует ужасные текущие потери. Тем не менее, эти голубые фишки должны торговаться на этих уровнях, ибо они максимизируют потенциальную геометрическую прибыль по отношению к дисперсии (риску), а также обеспечивают достижение цели в наикратчайшее время. С этой точки зрения, торговля голубыми фишками не более рискованна, чем торговля свиной грудинкой, которая ничуть не менее консервативна, чем торговля акциями голубых фишек. То же самое можно сказать о торговых системах, работающих с товарным портфелем и портфелем облигаций.
Обычно инвесторы практикуют разжижение либо намеренно, либо нет. То есть если в оптимальном варианте нужно торговать некоторым компонентом портфеля на уровне f$, скажем, 2500, то они могут намеренно торговать им на уровне f$, скажем, 5000, сознательно пытаясь сгладить кривую торгового капитала и сдемпфировать текущие потери, или бессознательно, на таких полуоптимальных уровнях f, значения которых могут быть определены для любой позиции, как это подробно описано в Главе 1.
Другой способ, который можно использовать при распределении капитала, – это разделение торгового капитала на два субсчета: активный субсчет и неактивный субсчет. Они не являются двумя отдельными счетами; напротив, теоретически, они олицетворяют способ разделения единственного счета.
Данный метод используется следующим образом. Прежде всего, вы должны выбрать начальное соотношение долей разделения. Давайте предположим, что изначально вы хотите имитировать счет на уровне половины от f. Поэтому уровень вашего начального сечения равен 0,5 (начальный уровень дробления должен быть больше 0 и меньше 1). Это значит, что вы будете делить свой счет так, что 0,5 капитала пойдет на пассивный субсчет, а 0,5 – на активный субсчет. Давайте предположим, что мы начинаем со счетом в 100 000 долл. То есть изначально 50 000 долл. будут на пассивном субсчете и 50 000 долл. – на активном субсчете. Именно средства на активном счете используются при определении того, сколькими единицами торговать. Эти субсчета в действительности не существуют; они являются гипотетической конструкцией, созданной вами для того, чтобы управлять своими деньгами более эффективно. В данном методе вы всегда используете полностью оптимальное f. Всякое изменение капитала отражается только на активной части счета. Поэтому вы должны ежедневно из общей величины счета (закрытые и открытые позиции в пересчете по текущим рыночным ценам) вычитать величину пассивных средств (она будет неизменной изо дня в день). Эта разность является вашими активными средствами, и по ней вы будете определять количество единиц для торговли на уровне f.


Предположим, что оптимальный уровень f торговли для рыночной системы А составляет один контракт на каждые 2500 долл. счета. В первый день вы начали с 50 000 долл. активных средств и, следовательно, будете торговать двадцатью единицами. Если бы вы следовали простой тактике половинной f, то в первый день вы торговали бы тем же количеством единиц. При половинном f вы торговали бы одним контрактом на каждые 5000 долл. средств на счете (2500 долл./0,5) и исходили бы из всех 100 000 долл. счета при определении того, сколькими единицами торговать. Поэтому, следуя тактике половинного f вы в этот день также торговали бы двадцатью единицами.
Однако как только величина счета изменяется, количество единиц, которым вы будете торговать, также изменяется. Предположим, что в этот день вы заработали 5000 долл., увеличив таким образом общую величину вашего счета до 105 000 долл. При тактике половинного f вы теперь будете торговать двадцать одной единицей. А по методу дробления счета вы должны вычесть неизменные 5000 долл. пассивной доли из всего капитала в 105 000 долл. Это даст 55 000 долл. активной доли, исходя из которой вы определите, что размер вашей позиции на оптимальном по f уровне даст один контракт на каждые 2500 долл. счета. Следовательно, по методу дробления счета вы теперь будете торговать двадцатью двумя единицами.
Данная процедура действует аналогичным образом и при понижении кривой капитала, то есть метод дробления счета быстрее сокращает количество торгуемых единиц, чем при тактике дробления f. Допустим, мы потеряли 5000 долл. в первый день торговли, сократив таким образом общую величину счета до 95 000 долл. Согласно тактике дробления f мы теперь стали бы торговать девятнадцатью единицами (95 000 долл./5000 долл.). В то же время по методу дробления счета вы, имея 45 000 долл. активных средств, будете торговать восемнадцатью единицами (45 000 долл./2500 долл.).
Обратите внимание, что при следовании методу дробления счета точная доля оптимального f, которую мы используем, меняется с изменением капитала. Мы определяем ту долю, с которой хотим начать. В нашем примере мы использовали начальное дробление пополам. Когда капитал увеличивается, эта доля оптимального f также растет, приближаясь в пределе к 1 при стремлении величины счета к бесконечности. Когда величина счета уменьшается, эта доля приближается к 0 в пределе на том уровне, где общий торговый капитал равняется своей пассивной части. Это обстоятельство, а именно наличие встроенного механизма страхования портфеля при дроблении счета, являющееся громадным преимуществом, мы подробно обсудим в данной главе далее.
Поскольку методу дробления счета отвечает изменяющаяся доля f, мы будем называть его методом динамического дробления f, в отличие от тактики простого дробления f (которую будем называть статическим дроблением f).
Использование метода динамического дробления f аналогично торговле на оптимальном уровне f при начальной величине счета, равной активной доле капитала.
Таким образом, мы видим, что существует два способа разбить счет относительно по-настоящему геометрически оптимального портфеля. Мы можем торговать статически дробным или динамически дробным f. Хотя оба этих метода взаимосвязаны, они также и различаются. Какой из них лучший?
Для начала нам нужно уметь определять арифметическое среднее HPR для одновременной торговли п данными сценарными спектрами, а равно дисперсию этих же HPR для данных значений f1... fn, сопоставленных этим сценарным спектрам. Теперь они задаются в виде:

Формула [5.01] просто суммирует значения HPR с коэффициентами, равными их вероятностям, и делит все это на сумму вероятностей.
Для определения дисперсии значений HPR данного набора нескольких одновременных сценарных спектров, торгуемых при данных значениях f, возьмем сначала грубый коэффициент от HPR:
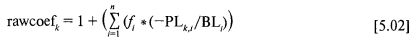
Затем эти грубые коэффициенты усредняются по всем значениям к между 1 и m и получается их среднее арифметическое:
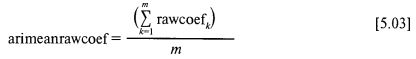
Теперь можно определить дисперсию V:
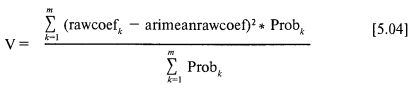
Здесь снова Probk определяется по формуле [4.03].
Зачем нам все это нужно? Если припомнить фундаментальное уравнение из Главы 1, то знание среднего арифметического HPR и дисперсии этих HPR может быть весьма полезным, что мы сейчас и продемонстрируем.
Если мы знаем, каковы значения AHPR и дисперсии на данном уровне f (скажем, для определенности, на уровне оптимального f), то мы можем использовать эти значения в торговле на уровне разбавления, который мы будем называть FRAC. И, поскольку мы можем вычислить эти две стороны прямоугольного треугольника, то мы можем также определить и среднее геометрическое HPR на этом разбавленном уровне. Далее приводятся формулы для разбавленного AHPR, называемого FAHPR, разбавленного стандартного отклонения (являющегося просто квадратным корнем из дисперсии), называемого FSD, разбавленного среднего геометрического HPR, называемого FGHPR.
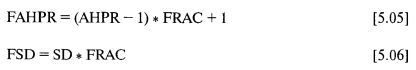

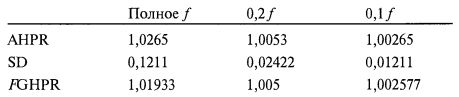
Предположим, что у нас имеется система, где AHPR равен 1,0265. Стандартное отклонение при этих HPR равно 0,1211 (т. е. – это квадратный корень из дисперсии, получаемой по формуле [5.04]); откуда расчетное среднее геометрическое равно 1,019. Теперь посмотрим, какими будут эти характеристики для статического дробления f на уровнях 0,2 и 0,1. Они таковы:
Вот еще одна формула, которая также окажется полезной, для определения ожидаемого времени достижения конкретной цели:

Теперь мы сравним торговлю согласно тактике статичного дробления f на уровне 0,2 и со средним геометрическим 1,005 с методом динамического дробления f на уровне 0,2 (при 20% начального активного капитала) и с дневным средним геометрическим 1,01933. Время (в количестве дней, поскольку используется дневное среднее геометрическое), потребное для удвоения статичного дробного f, согласно формуле [5.08а] равно:
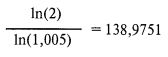
Для удвоения динамического дробного f потребуется установить цель на 6. Это так, поскольку, если изначально в работе задействуются 20% капитала, составлявшего вначале 100 000 долл., то сначала в работе у вас будет 20 000 долл. Цель состоит в том, чтобы довести активный капитал до 120 000 долл. Поскольку пассивный капитал остается равным 80 000 долл., тогда всего на вашем счете, где изначально было 100 000 долл., будет 200 000 долл. Следовательно, для увеличения счета с 20 000 до 120 000 долл. вам нужно достичь TWR, равного 6. Если для удвоения динамического дробления f на уровне 0,2 цель равняется 6, то:
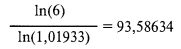
Обратите внимание, что при динамическом дроблении f потребуется 93 дня в отличие от 138 дней, потребных при статическом дроблении f.
Теперь займемся уровнем дробления 0,1. Ожидаемое количество дней для удвоения счета при статичном дроблении составит:
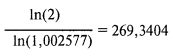
По сравнению с этим для удвоения при динамическом дроблении с начальной активной долей 0,1 потребуется достичь TWR, равного 11. Следовательно, потребное количество дней для сравнимого результата при динамическом дроблении составит:
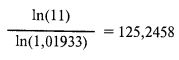
Таким образом, для удвоения капитала при уровне дробления f 0,1 в нашем статичном примере понадобится 269 дней против 125 дней, потребных при динамическом дроблении. Чем меньше доля f, тем быстрее динамический метод станет лучше статичного.
Рассмотрим утроение при дроблении f на уровне 0,2. Ожидаемое количество дней для утроения при статичном методе равно:
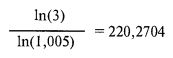
По сравнению с этим динамический аналог требует:
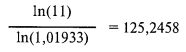
Для получения 400% прибыли (т. е. когда цель, или TWR, равно 5) при статическом методе на уровне 0,2 потребуется:
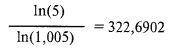
По сравнению с чем в динамическом варианте имеем:
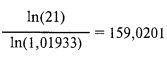
В этом примере для достижения цели в 400% динамический метод не занимает и половины того времени, которое нужно при статическом методе. Кроме того, если поинтересоваться, какое TWR будет через 322,6902 дня, нужных для четырехкратного роста при статичном методе, то получим:

Это означает получение 9600% за то время, которое уходит на получение 400% при статичном методе.
Теперь можно изменить формулу [5.08а], чтобы приспособить оба метода дробления f для определения ожидаемой длительности, требуемой для достижения конкретной цели в терминах TWR. Начнем с выражения [5.08б] для статичного дробления f:

Для динамического дробления f имеем выражение [5.08с]:
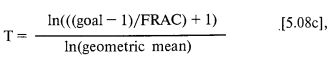
где:
Т = ожидаемое количество периодов владения, нужных для достижения конкретной цели;
goal = цель в терминах множителя к начальному капиталу, TWR;
FRAC = начальная доля активного капитала;
среднее геометрическое = грубое среднее геометрическое HPR при оптимальном f (здесь не используется корректировка, подобная той, что в выражении [5.086]);
ln( ) = функция натурального алгоритма.
Итак, для иллюстрации использования формулы [5.08с] предположим, что мы хотим определить, сколько времени уйдет на удвоение счета (т. е. для получения TWR = 2) при активной доле капитала 0,1 и среднем геометрическом 1,01933:

То есть если наши средние геометрические определены для сценариев, периоды владения которых исчисляются в днях, то мы можем ожидать удвоения примерно через 125 1/4 дней. Если наши сценарии используют периоды владения, исчисляемые в днях, то мы ожидали бы удвоения через 125 1/4 месяцев.
Пока вы имеете дело с такими Т, которые достаточно велики для того, чтобы значение [5.08с] превышало значение [5.086], вы выгадаете от использования в торговле метода динамического дробления f. Это можно также выразить в виде [5.09]:
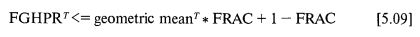
To есть вы должны итеративно перебирать значения Т, пока правая часть этого выражения не станет больше ее левой части, это и будет то значение Т (количество периодов владения), которое следовало бы подождать до перераспределения портфеля. До этого будет лучше торговать на основе статичного дробления f.
На рис. 5.1 это иллюстрируется графически. Стрелкой отмечено то значение Т, при котором правая сторона [5.09] равна левой стороне.
Таким образом, если используемая нами активная доля капитала равна 20%, то есть FRAC = 0,2, то FGHPR следует рассчитывать на основе 0,2 f. Поэтому для случая, когда наше среднее геометрическое при полном оптимуме f равно 1,01933 и 0,2 f (FGHPR) равно 1,005, нам нужно значение Т, удовлетворяющее следующему условию:
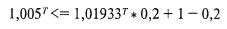
Мы определили наше среднее геометрическое для оптимального f, а значит, и наше среднее геометрическое для дробного f (FGНPR), применительно к периодам владения, измеряемых в днях. Желательно было бы знать, хватит ли нам квартала. Поскольку в квартале содержится около шестидесяти трех торговых дней, нам нужно определить, будет ли Т, равное шестидесяти трем, достаточным временем для того, чтобы выгадать от использования динамического дробления f. Поэтому проверим, что дает выражение [5.09] при подстановке в качестве Т величины шестьдесят три:

Поскольку в данном случае левая часть меньше правой, то условие [5.09] выполнено. Следовательно, при заданных параметрах мы можем перераспределить портфель через квартал и воспользоваться преимуществами динамического дробления f.
На рис. 5.1 показано соотношение между торговлей на основе методов статичного и динамического дробления f в зависимости от истекшего времени.
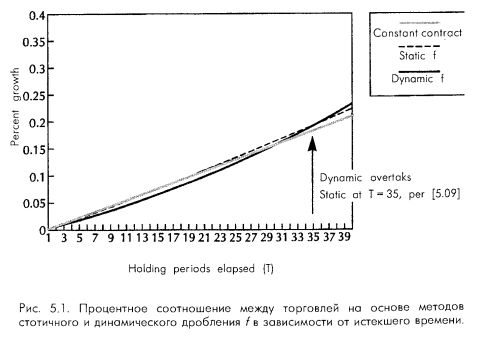
Данный график иллюстрирует торговлю с начальной активной долей капитала в 20% как на статичной, так и на динамичной основе. Оба варианта начинаются с одинакового количества единиц, поэтому именно это количество единиц, как постоянный контракт, торгуется все периоды владения. Среднее геометрическое HPR при полном f, используемом в этом примере, было равно 1,01933, а среднее арифметическое HPR было равно 1,0265. Отсюда среднее геометрическое при статичном дробном f на уровне 0,2 было равно 1,005.
Из всего этого следуют два важных момента: динамичное дробление f опережает статичное дробление f тем быстрее, чем меньше активная доля и чем больше среднее геометрическое. То есть при использовании начальной активной доли капитала величиной 0,1 (для статичного и динамичного методов) динамичный метод быстрее превзойдет статичный метод, чем при использовании доли величиной 0,5. Поэтому обычно метод динамичного дробления f тем скорее превзойдет статичный вариант, чем меньше начальная доля активного капитала. Другими словами, портфель с начальной активной долей капитала величиной 0,1 скорее станет лучше своего статичного варианта, чем портфель с начальной долей в 0,2 станет лучше своего статичного варианта. При начальной активной доле капитала в 100% (1,0) динамичный метод никогда не превзойдет статичного (скорее, они будут давать одинаковый прирост). Кроме того, на скорость, с которой динамичный метод становится лучше статичного, влияет среднее геометрическое самого портфеля. Чем больше среднее геометрическое, тем скорее метод динамичного дробления превзойдет статичный вариант. При среднем геометрическом 1,0 динамичный вариант никогда не станет лучше статичного.
Чем больше истекшего времени, тем больше разница между методами статичного и динамичного дробления f. Асимптотически метод динамичного дробления f приносит значительно больший капитал, чем метод статичного дробления.
Наконец, еще один важный момент, касающийся рис. 5.1. Линия постоянного контракта пересекает две других линии раньше, чем они пересекутся друг с другом.
В конечном итоге большую выгоду приносит распределение капитала с использованием метода динамичного дробления f. То есть вы определяете начальный уровень – процент – для размещения в качестве активного капитала. Остаток – это пассивный капитал. Ежедневные изменения капитала отражаются только на его активной доле. Пассивная долларовая величина остается неизменной. Поэтому вы ежедневно вычитаете из вашего общего капитала на счете его пассивную часть. Получаемая разница составляет активную часть капитала, по которой вы будете определять объемы вашей торговли с использованием оптимальных уровней f.
Теперь, когда рассчитывается требование по доходности позиций, оно не будет точно таким же, как ваш активный капитал. Оно может быть больше или меньше – роли это не играет. То есть если только ваше требование по доходности не составляет 100% капитала на счете, то в каждом данном периоде владения у вас на счете будет определенная неиспользуемая наличность. Следовательно, вы почти всегда ненамеренно размещаете что-то в наличности (или в эквиваленте наличности). Очевидно, что при этом нет никакой нужды в сценарном спектре, предусматривающем переход в наличность или ее эквиваленты, – в наличность уже делается должное вложение, когда вы выделяете активную и пассивную части капитала.
|