Управление текущими потерями и новая методология
Большие текущие потери происходят по трем причинам. Первая и наиболее распространенная из них – это катастрофический проигрыш на одной сделке. Я пришел в этот бизнес в качестве маржевого клерка, задачей которого было отслеживать состояние сотен счетов. Я поработал программистом и консультантом на многих крупнейших трейдеров мира. Я торговал и прорабатывал проблемы в области торговли всю мою взрослую жизнь, зачастую наблюдая с птичьего полета за тем, как люди действуют на рынках и в смежных сферах. Я был свидетелем того, как множество людей были уничтожены в течение одной сделки. Кроме того, у меня есть большой собственный опыт поражения на единственной сделке.
Общим знаменателем во всех случаях, когда такое происходит, является недостаточная ликвидность рынка. Важность ликвидности нельзя переоценить. Ликвидность не есть что-то такое, что мне удалось оценить количественно. Это не просто некая функция открытого интереса и объема. К тому же, ликвидность вовсе не должна испаряться надолго, чтобы нанести огромный вред. Фьючерсы на казначейские облигации США были самыми ликвидными контрактами в мире в 1987 г. Однако и они оказались совершенно неликвидными на несколько дней в октябре 1987 г. В отношении ликвидности вы должны быть постоянно на чеку.
Второй путь, который ведет людей к крупным потерям, даже более трагичен, но не менее распространен. На него приводит незнание своей позиции на рынке до того, как он безжалостно двинется против нее. Это трагично потому, что этого всегда можно избежать. Однако это распространенное явление. Вы всегда должны знать свои позиции на каждом рынке.
Третьей причины потерь боятся больше всего, хотя она приводит к тем же последствиям, что и первые две причины. Потеря этого типа характеризуется затяжной полосой проигрышей, между которыми иногда могут вклиниваться несколько выигрышных сделок. Это тот тип потерь, перед которыми большинство трейдеров живут в постоянном страхе. Потери этого типа заставляют системных трейдеров задаваться вопросом, работают ли все еще их системы. Но именно этот тип потерь поддается управлению и значительному сокращению с помощью нашей новой методологии.
Новая методология в распределении активов сосредоточивается на оптимальности роста. Однако для сообщества управляющих капиталом вопросы оптимальности роста стоят, как правило, на втором месте. Основная забота – сохранение капитала.
Это верно не только для управляющих капиталом, но также и для большинства инвесторов. Сохранение капитала основывается на сокращении потерь. Предложенная нами новая методология впервые позволяет свести деятельность по минимизации потерь к математической задаче. Как ни парадоксально, это одно из многих неожиданных следствий новой методологии.
Все написанное мной и ранее, и в этой книге касается оптимальности роста. Впрочем, разрабатывая методологию под углом зрения оптимальности роста, в ее же рамках мы можем взглянуть на вещи и с позиций оптимизации потерь. Выводы, которые следуют из новой методологии, нельзя было бы получить на иной основе.
Идея оптимального f, которая вылилась в эту новую методологию распределения активов, теперь может выйти за рамки теоретических формулировок и концепций в область практического применения с прицелом на достижение целей управляющих капиталом, а равно и инвесторов.
Старые среднедисперсионные модели были плохо приспособлены для реализации идеи управления потерями. Первой причиной этого является то, что риск сводился к упрощенному представлению в виде дисперсии доходов. Причем возможно, и в действительности довольно часто, сократить дисперсию дохода, однако не сократить сами потери.


Представьте себе два компонента, отрицательно скоррелированных друг с другом. Компонент 1 растет по понедельникам и средам, но падает по вторникам и четвергам. Компонент 2 ведет себя точно противоположным образом и падает по понедельникам и средам, но растет по вторникам и четвергам. По пятницам обе компоненты падают. Торговля обеими компонентами вместе сокращает дисперсию дохода, однако в пятницу понесенные потери могут быть на деле больше, чем при торговле только одним из двух компонентов. В конце концов, все корреляции сводятся к одной. Модель средней дисперсии не ориентирована на потери и просто минимизирует дисперсию дохода. Хотя она может отсечь многие потери, она все же оставляет вас беззащитными перед серьезными потерями.
Рассмотрение потерь с позиций новой методологии все же даст нам некоторую очень полезную информацию. Задумайтесь на минуту о том, что потери минимизируются путем отказа от торговли (т. е. при f = 0). То есть если мы обратимся к случаю двух одновременных игр в монетку «два-к-одному», то рост максимизируется при f, равном 0,23 для каждой игры, в то время как потери минимизируются при f, равном 0 для обеих игр.
Первым важным моментом в понимании оптимальности потерь (т. е. минимизации потерь) является то, что к ней можно приблизиться в торговле. Оптимальная точка, в отличие от точки оптимального роста, не может быть достигнута никак иначе, чем путем отказа от торговли. Но к ней можно приблизиться. Таким образом, для минимизации потерь, то есть для приближения к оптимальности потерь, требуется использовать для каждой компоненты минимально возможные значения f. Другими словами, для того чтобы приблизиться к оптимальности потерь, вы должны присесть в том углу поверхности, где значения всех f близки к 0.
На рис. 5.11, изображающем нечто похожее на игру в монетку «два-к-одному», пик никуда не перемещается. Это теоретически идеальный случай, и, как таковой, он может использоваться в качестве модели совершенного портфеля для сравнения с обычными моделями.
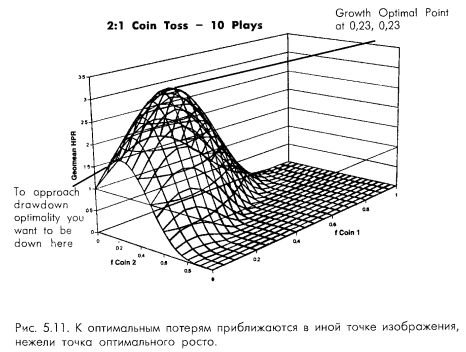
Впрочем, как упоминалось ранее, в реальном мире торговли рынки не согласуются столь четко с теоретическим идеалом. Дело в том, что в отличие от рассмотренных игр в монетку «два-к-одному» распределение доходов со временем меняется при изменении условий на рынке. Поверхность обладает способностью к реконфигурации и перемещается в разных направлениях при изменении условий на рынке. Чем ближе вы находитесь к пику, тем драматичнее это скажется на потерях при ее перемещении уже просто потому, что поверхность имеет наибольшую крутизну ближе всего к пику. Если бы мы вычертили карту поверхности вроде той, что изображена на рис. 5.11, но только по данным за период, когда обе системы приносили убытки, то поверхность (высота, или TWR) была бы на отметке 1,0 в f-координатах (0; 0), а далее параболически соскальзывала бы оттуда.
Мы приближаемся к оптимальности потерь по тем f, которые близки к 0 по всем компонентам. В случае поверхности, изображенной на рис. 5.11, нам было бы лучше переместиться в левый верхний угол поблизости от 0 по значениям всех f. Причина этого в том, что когда плоскость изгибается и пик смещается в стороны, негативный эффект от этого в данном углу будет самым минимальным. Другими словами, при изменении ситуации на рынке отрицательные последствия для трейдера в этом углу минимизированы.
Может создаться обманчивое впечатление, что при этом в жертву приносится рост, который уменьшается по экспоненте. Развеять эти опасения можно с помощью фундаментального уравнения торговли. Поскольку рост, или TWR, представляет из себя среднее геометрическое доходов за периоды владения, возведенное в степень Т, то количество конов игры можно получить из формулы:

В вышеуказанном углу значение G гораздо меньше. Но с увеличением Т мы сталкиваемся с экспоненциальным уменьшением роста, представляющего собой экспоненциальную функцию.
Короче говоря, если трейдеру нужно минимизировать потери, то ему выгоднее торговать при очень малых значениях f и задействовании много большего количества периодов владения на одном том же отрезке времени.
Рассмотрим, например, разыгрывание только одной игры в монетку «два-к-одному». После 40 периодов владения при f = 0,25 среднее геометрическое HPR равно 1,060660172, a TWR равно 10,55. Если бы мы играли в ту же самую игру при значении f 0,01, то наше среднее геометрическое HPR было бы равно 1,004888053, что превысило бы 10,55 при возведении в степень 484. Таким образом, если можно сыграть 484 кона (периода владения) за то же время, которое ушло бы на 40 конов, то это дало бы эквивалентный рост при резком сокращении в потерях. К тому же вы значительно оградили бы себя от изменений поверхности. То есть вы одновременно весьма защитились бы и от изменений ситуации на рынке.
Может показаться, что вам понадобится торговать более чем одним компонентом (т. е. сценарным спектром) одновременно. То есть что для увеличения Т нужно торговать много большим количеством компонентов одновременно. Это противоречит мысли, высказанной ранее при обсуждении точек перегиба, что может оказаться выгоднее торговать только одним компонентом. Но, увеличивая количество компонентов, торгуемых одновременно, вы увеличиваете составное /портфеля. Например, если бы вы одновременно торговали по 20 сценарным спектрам f = 0,005 для каждого, то ваше составное f для всего портфеля было бы равно 0,1. На данном уровне одновременная реализация наихудших сценариев привела бы к потере 10% капитала. И напротив, вы преуспели бы больше, торгуя только по одному сценарному спектру, если бы могли задействовать эквивалент 20 периодов владения за тот же самый отрезок времени. Это может оказаться невозможным, но это – направление, в котором вы стали бы действовать для минимизации потерь.
Наконец, когда трейдер старается приблизиться к минимизации потерь, он может при этом использовать идею постоянного доминирования. Постоянное доминирование прекрасно для теоретически идеальной модели. Однако оно весьма чувствительно к изменениям поверхности. То есть при изменении исходных сценариев для подстройки к изменяющимся характеристикам рынка постоянное доминирование начинает сбоить. В азартной игре, где условия не изменяются от одного периода к другому, постоянное доминирование идеально. В реальном мире торговли вы должны защитить себя от колебаний поверхности. Поэтому минимизация потерь в рамках новой методологии очень хорошо приспосабливается к внедрению постоянного доминирования.
Итак, теперь мы завершили полный цикл от рассмотрения поверхности в пространстве рычагов и отыскания точки оптимального роста на ней до отступления от этой точки во имя удовлетворения реальных основополагающих ограничений по части минимизации потерь и сохранения капитала. Просто увеличив показатель степени тем или иным доступным образом, мы достигаем роста. Мы, возможно, достигнем эквивалентного роста, если сможем добиться достаточно большого Т, или достаточно высокого показателя степени. Поскольку показатель степени равен количеству периодов владения за данный отрезок времени, мы постараемся задействовать максимально возможное количество периодов владения за данный отрезок времени. Но при этом вовсе не обязательно торговать по максимально возможному количеству сценариев. Все корреляции приводят к одной. К тому же мы должны постоянно допускать случай, когда наихудшие сценарии реализуются одновременно для всех торгуемых компонент. Мы должны учитывать, что составное f, или сумма значений f для всех одновременно торгуемых компонентов, представляет собой потери, которые нам предстоит перенести. Отсюда вытекает, что, стараясь приблизиться к оптимальности потерь, но и стремясь получить такой же рост, как и в оптимальной точке роста, следует торговать по минимально возможному количеству компонент и при минимально возможных значениях f для каждого компонента, а также добиваться задействования максимально возможного количества периодов владения за данный отрезок времени.
Точка оптимального роста – опасное место локализации. Но точно определив ее, то есть если мы располагаемся на том месте, где будет пик, то мы можем получить колоссальный рост. Даже в этом случае нам предстоит пережить серьезные потери. Впрочем, методология пространства рычагов позволяет нам выбрать такое место на карте в пространстве рычагов, где будет достигнута минимизация потерь. Это далее откроет нам альтернативный путь к достижению роста с помощью увеличения Т, или показателя степени, любыми доступными способами. Математически данная стратегия не столь очевидна с методологических позиций, известных прежде.
|