6.4.2. Метод ведущих факторов
С учетом подходов, развиваемых в рамках традиционного фундаментального анализа для рынка ценных бумаг (см. разд. 6.2), можно предположить, что эффективность ценных бумаг, определяемая формулой 6.4.1, будет зависеть от целого ряда факторов. Например, от финансового положения эмитента ценных бумаг, отрасли, в которой он осуществляет свою деятельность, и многих других факторов, включая даже такие непосредственно не измеряемые, как успешность рекламно-маркетинговой компании при продаже ценных бумаг и так далее. Принципиально методами факторного анализа, использование которого применительно к фондовому рынку рассмотрено, например, в работе, можно оценить значимость и влияние любых факторов на эффективность ценных бумаг.
Применительно к западному фондовому рынку (США) было эмпирически замечено, а также позже подтверждено многочисленными статистическими исследованиями, что главным ведущим фактором, определяющим эффективность ценных бумаг, является состояние рынка в целом. Состояние рынка в целом является «барометром», позволяющим предсказывать судьбу ценных бумаг на рынке и это состояние рынка отражается в сводных индексах Доу-Джонса, Standart and Poor's Index (S&P 500 Index) и других индексах. Наиболее важным для финансовых аналитиков является S&P 500 Index, представляющий собой сумму курсов 500 важнейших видов ценных бумаг, взвешенных с учетом акционерного капитала каждой корпорации. В теории финансового рынка аналогичную роль играет величина, именуемая эффективностью рынка в целом и представляющая собой взвешенную (с учетом капитала) сумму эффективностей всех рисковых ценных бумаг, функционирующих на рынке. Это совершенно очевидно, если подставить два смежных значения S&P 500 индексов в формулу (6.4.1). Все расчёты индексов рынка для ценных бумаг США осуществляются на регулярной основе специализированными фирмами, например Merril Lynch and Co., Ltd, и публикуются в специальных изданиях. В качестве временного горизонта представления статистических данных используются котировки ценных бумаг за 5 лет, предшествующих дате расчёта индекса, при этом используется поквартальная дискретизация информации.


Выделение ведущего фактора позволило построить простые и удобные для конечных пользователей математические модели (в рамках линейного регрессионного анализа) для оценивания динамики эффективностей ценных бумаг в функции состояния рынка в целом. В распоряжение конечного пользователя предоставляется модель линейной регрессии в виде:

где:
i – номер ценной бумаги;
Yi – эффективность i-й ценной бумаги, «отклик» или, что одно и тоже, объясняемая переменная;
Хm – текущее значение эффективности рынка в целом, рассчитываемое по формуле (6.4.1) на основе публикаций индексов рынка (например, S&P 500 Index), Хm является входной переменной;
ai, bi – коэффициенты линейной регрессионной модели для i-й ценной бумаги; эти коэффициенты, а также относительные ошибки их вычисления публикуются в специальных изданиях для ценных бумаг, функционирующих на рынке.
На основе модели (6.4.4) конечный пользователь, подставляя текущее или прогнозируемое значение эффективности рынка Хт (рассчитываемое по формуле (6.4.1) или же публикуемое в специальных изданиях), легко может рассчитать текущую или прогнозируемую эффективность i-й ценной бумаги и уже на основе этого может принимать экономически обоснованные решения.
На практике более удобно отсчитывать эффективность ценных бумаг относительно эффективности безрискового вклада R0. Эффективность безрисковых вложений (ставка без риска) играет важную роль в теории равновесия на конкурентном финансовом рынке. Центральное место в этой теории занимает регрессионная модель У. Шарпа, известная как модель установления цен на капитальные активы (Capital Asset Pricing Model, САРМ). В рамках указанной модели основное уравнение равновесного рынка имеет вид:
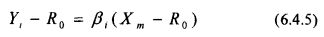
В выражении (6.4.5) расшифровка основных обозначений приведена ранее. Новый коэффициент пропорциональности βi в выражении (6.4.5) играет важную роль в финансовом анализе и называется «бета ценных бумаг вида i относительно рынка» или же «бета i-го вклада». Левая часть в выражении (6.4.5), в виде превышения величины эффективности рискованных вложений над эффективностью безрискового вклада, называется премией за риск.
Если значение βi положительно, то эффективность i-й ценной
бумаги прямо пропорционально эффективности рынка. Если значение βi отрицательно, то эффективность i-й ценной бумаги будет снижаться при возрастании эффективности рынка.
Премия за риск от вложения i-й ценной бумаги линейно зависит от ситуации, складывающейся на рынке.
Модели линейной регрессии (6.4.4 – 6.4.5), с одной стороны, очень просты и это является их достоинством, но с другой стороны их простота оборачивается потерей точности предсказаний из-за не учёта ведущего фактора (состояния рынка в целом) и других факторов, влияющих в той или иной степени на эффективность ценных бумаг. Учёт нескольких факторов, безусловно, можно осуществить в рамках моделей множественной линейной или же нелинейной регрессии, но это усложнит для конечного пользователя вид моделей и обозримость результатов. Поэтому для того, чтобы повысить точность предсказания модели линейной регрессии для всего спектра ценных бумаг, функционирующих на рынке США, пошли не по пути усложнения моделей, а путём введения дополнительных поправок к коэффициентам линейной регрессии в моделях (6.4.4 – 6.4.5). Статистические исследования рынка США показали, например, что эффективной для коррекции коэффициента βi в выражении (6.4.5) является формула:
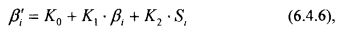
где:
β'i – скорректированный коэффициент линейной регрессии;
К0, К1, К2 – некоторые коэффициенты, а значение Si – это
десятичный логарифм суммарной стоимости компании, для которой осуществляется прогнозирование в рамках модели (6.4.5).
Параметры моделей линейной регрессии типа (6.4.4 – 6.4.5), а также оценки точности указанных моделей, в виде среднего квадрата ошибок и среднеквадратического отклонения ошибок, публикуются в США в специальных изданиях.
Результаты прогнозирования эффективностей ценных бумаг по моделям типа (6.4.4 – 6.4.6), а также значения ошибок прогнозирования («риски» ценных бумаг) могут использоваться в качестве исходных данных для последующей оптимизации портфеля ценных бумаг. Ниже вкратце рассмотрим основные количественные характеристики и свойства портфеля ценных бумаг в зависимости от номенклатуры входящих в него бумаг. Кроме того, рассмотрим также основные классические постановки задач по оптимизации портфеля ценных бумаг.
|