6.4.5. Классические постановки задач оптимизации портфеля ценных бумаг

Ниже приведены классические постановки и качественные результаты, следующие из решения задач формирования оптимального портфеля, составленного из рискованных ценных бумаг, смеси рискованных и безрисковых ценных бумаг. Первый тип задач впервые рассматривался Г. Марковицем, а второй тип Д. Тобиным.

Кроме того, кратко рассмотрена стратегия формирования портфеля, называемая логарифмической стратегией Келли.

а) Задача формирования оптимального портфеля, составленного только из рискованных ценных бумаг

С учетом терминологии (см. выше раздел 6.4.3), определяющей количественные характеристики портфеля ценных бумаг в виде математического ожидания эффективности портфеля (6.4.9) и дисперсии эффективности портфеля (6.4.12), формулировка задачи оптимизации портфеля выглядит следующим образом.

Пусть X_j – доля от вложения капитала, приходящаяся на j-й вид ценных бумаг. Требуется найти доли X_j, соответствующих вложений в те или иные ценные бумаги, обеспечив при этом минимальное значение ковариации эффективности портфеля («риска») и при условии обеспечения заданного значения эффективности портфеля в целом. В векторно-матричных обозначениях задача оптимизации портфеля ценных бумаг имеет вид:

где (6.4.27) – это оптимизируемая целевая функция, а выражение:

задает требуемое значение уровня эффективности портфеля ценных бумаг.

Выражение:

является условием нормировки искомых переменных X_j, поскольку они являются долями от единицы и в сумме должны составлять единицу.

В выражениях (6.4.27-6.4.29) приняты следующие обозначения:

V = [V_{i, j}] – матрица ковариации эффективностей ценных бумаг размерности NxN;
m = [m_j] – вектор-столбец ожидаемой эффективности (математического ожидания), координатами которого являются эффективности финансовых инструментов;
I[1] – единичный вектор-столбец;
X = [X_j] – вектор-столбец неизвестных (искомых) пропорциональных долей вложения в те или иные ценные бумаги;

Знаком Т здесь и везде далее по тексту обозначена операция транспонирования.

В указанном виде задача оптимизации (6.4.27-6.4.29) может быть решена, например, с помощью метода неопределенных множителей Лагранжа. Указанный приём позволяет свести задачу на условный экстремум целевой функции (6.4.27), при ограничениях (6.4.28-6.4.29), к задаче на безусловный экстремум. Однако, в этом случае некоторые из искомых переменных могут оказаться отрицательными, что означает рекомендацию взять в долг ценные бумаги j-го вида в количестве X_j, т.е. провести операцию «продажа без покрытия». Если взятие в долг ценных бумаг невозможно, то дополнительно к условиям задачи (6.4.27-6.4.29) необходимо добавить условие неотрицательности искомых переменных, то есть:

для вcex j.

В этом случае задача оптимизации (6.4.27 – 6.4.30) может быть решена методами нелинейного программирования.

Из постановки задачи оптимизации в виде (6.4.27 – 6.4.30) очевидны следующие качественные результаты:

- предельная ожидаемая эффективность портфеля ценных бумаг не может превысить эффективности ценной бумаги, имеющей максимальное значение. Если в выражении (6.4.28) задан уровень эффективности больше предельного (максимального) значения эффективности ценных бумаг, то задача не имеет решения;

- если заданное значение уровня эффективности портфеля в выражении (6.4.28) равно самому большему значению, которое, допустим, имеет j-й вид ценных бумаг, то в оптимальный портфель будет входить только j-й вид ценных бумаг;

- пусть уровни эффективности всех имеющихся на рынке ценных бумаг проранжированы в порядке их убывания. Тогда, если заданное значение уровня эффективности портфеля в выражении (6.4.28) больше или равно эффективности второго по величине члена проранжированного по эффективностям ряда, то в оптимальный портфель будет входить не более двух ценных бумаг с наибольшими значениями эффективности. Пропорциональное соотношение между этими двумя видами ценных бумаг будут выбираться исходя из минимума значения целевой функции (6.4.27) и так далее.

б) Задача оптимизации портфеля, составленного из рисковых и безрисковых ценных бумаг

Формальная постановка задачи оптимизации смешанного портфеля ценных бумаг имеет вид:

В выражениях (6.4.31-6.4.34) приняты точно такие же обозначения, как и в постановке задачи оптимизации рискованного портфеля (см. выше), а также приняты дополнительно обозначения: r₀ – вектор-столбец эффективности вложений в безрисковые ценные бумаги; X₀ – вектор-столбец, состоящий из долей капитала, вкладываемого в безрисковые ценные бумаги.

Д. Тобиным показано, что задача оптимизации 6.4.31-6.4.34 решается проще, чем задача оптимизации чисто рискового портфеля. Для комбинированного портфеля, состоящего из рискованных и безрисковых ценных бумаг, решение может быть получено в аналитической форме с помощью метода неопределенных множителей Лагранжа.

Последовательность решения задачи состоит в том, что первично необходимо задаться соотношением рисковой и безрисковой частей портфеля, а затем уже для выбранного соотношения определяется оптимальная структура рискованной части портфеля.

в) Логарифмическая стратегия Келли для оптимизации портфеля ценных бумаг

В указанном методе в качестве критерия оптимальности портфеля выбраны средние темпы роста будущей доходности вложений. Под будущей доходностью портфеля понимается отношение его стоимости через время t к его начальной стоимости. Обозначим через S₀ – начальную стоимость портфеля, а через S_t – стоимость портфеля через время t. Обозначим через P_i коэффициенты, характеризующие доходность, при этом P₀ – доходность безрискового вложения. Если P_i = 1, то i-й финансовый инструмент не приносит прибыли, если P_i < 0, то финансовый инструмент является убыточным и если P_i > 0, то финансовый инструмент является прибыльным.

С учетом этого, постановку задачи оптимизации портфеля с использованием стратегии Келли можно представить в виде:

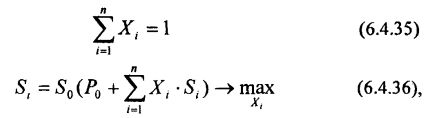где S_i = P_i – P₀. Обозначив через Z = S_i / S₀, целевую функцию 6.4.36 в рамках логарифмической стратегии оптимизации Келли можно переписать в виде:

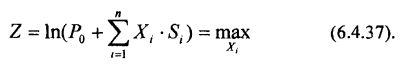
Существует также ряд преимуществ стратегии Келли перед другими стратегиями оптимизации. В частности, стратегия Келли оптимальна в том смысле, что время достижения любого заранее заданного уровня доходности портфеля при её использовании минимально. Другое преимущество стратегии Келли по сравнению со стратегией Г.Марковица состоит в том, что в ней используется стохастическое прогнозирование будущей доходности портфеля.

Содержание

Далее