7.2.2. Задача оптимального программного управления динамической системой
Под динамическими системами понимаются такие системы, модель функционирования которых в функции времени может быть представлена в виде дифференциальных (для дискретного времени – разностных) уравнений.
В терминах теории управления задача оптимального ПРОГРАММНОГО управления динамической системой может быть сформулирована в следующем виде:
Требуется решить вариационную задачу, а именно найти функцию времени U(t) (т.е. «управление»), исходя из условия обеспечения экстремума целевому функционалу, т.е.:

Выражение (7.2.1) – это целевой функционал, конкретное содержание которого определяется выбираемой целью управления.
Выражение (7.2.2) – это векторно-матричное дифференциальное уравнение, описывающее динамику системы, которое может быть решено при начальном условии, определяемом выражением (7.2.3). Отметим, что вынужденную составляющую решения указанного уравнения определяет правая часть этого уравнения, а именно – управление U(t).
Выражение (7.2.4) определяет ограничения на управление U(t) динамической системой.


Отметим далее, что в зависимости от ВИДА ЦЕЛЕВОГО ФУНКЦИОНАЛА, задачи оптимального управления называют задачей Больца:
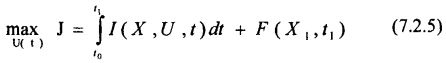
задачей Лагранжа:
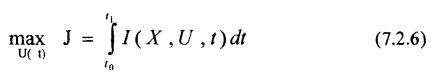
задачей Майера:
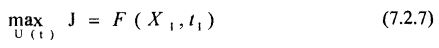
Задачи оптимального управления вне зависимости от вида целевого функционала могут быть преобразованы одна в другую и, в математическом смысле, являются полностью эквивалентными друг другу.
Задачу оптимального ПРОГРАММНОГО управления динамической системой также называют задачей оптимального управления динамической системой по РАЗОМКНУТОМУ контуру.
В задачах указанного типа никак не используется информация о текущем состоянии системы, и оптимальное управление может быть синтезировано заранее, т.е. без учета указанной информации.
Пример программного управления температурой жилого дома рассматривался нами ранее.
Еще одним примером задачи оптимального программного управления является определение оптимальной траектории движения ракеты. Управляющие параметры в этой задаче – это моменты включения двигателей и длительность их работы, величина и направление силы тяги, которую следует приложить к ракете в каждый отдельный момент времени. Режим работы двигателей выбирается в зависимости от ряда ограничений, например, в зависимости от общего количества топлива на борту ракеты. Вектор состояния указанной управляемой системы может отождествляться с массой ракеты, а также с ее траекторными координатами и скоростями их изменения. Зависимость вектора состояния системы в функции времени описывается системой дифференциальных уравнений, выводимых из законов механики. Результирующая траектория космического полета определяется в результате поиска экстремума целевого функционала, куда входит вектор состояния и управления ракетой. Например, при разработке проекта полета на Луну на ракете «Аполлон» в качестве цели управления выбиралась максимизация массы последней ступени ракеты, что математически отражалось выбором терминального целевого функционала Майера вида (7.2.7).
Блок-схема системы оптимального программного управления динамической системой, применительно к портфелю финансовых инструментов, представлена ниже на рисунке 7.1.
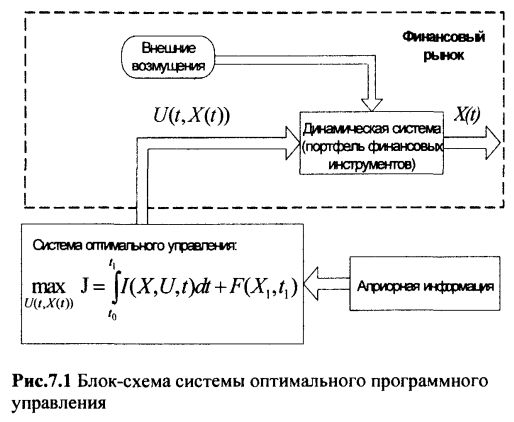
|