7.3.1. Связь между дифференциальными (разностными) уравнениями и корреляционными функциями случайных процессов
Для того, чтобы опираться на математические методы теории оптимального управления динамическими системами, надо предварительно показать концептуальную тождественность постановок задач оптимального управления применительно к финансовым и техническим системам. Предварительно покажем, что процессы функционирования таких динамических систем как летательные аппараты, с одной стороны и процессы функционирования финансового рынка, можно адекватно описывать с помощью одних и тех же математических моделей.
Как было отмечено выше, в постановках задач оптимизации для финансового рынка главным пунктом исходных предположений являлось то, что курсы обращающихся на финансовом рынке инструментов (в функции времени) являются реализациями случайных функций (для дискретного времени – случайных последовательностей). Это утверждение, с нашей точки зрения, не может вызвать особых сомнений, так как имеется множество работ, подтверждающих указанный факт. С другой стороны, применительно к задаче оптимального управления динамическими системами (например, всевозможными подвижными объектами) в качестве исходных данных для оптимизации должны быть заданы дифференциальные (для дискретного времени – разностные) уравнения для описания динамики объекта (системы).
Для доказательства возможности использования одинаковых математических моделей необходимо показать, каким образом для описания случайных процессов функционирования финансового рынка можно использовать дифференциальные (разностные) уравнения.
Возможность подобного описания применительно к финансовому рынку вытекает из следующих рассуждений.
Рассмотрим предварительно в концептуальном плане дифференциальные (для дискретного времени – разностные) уравнения, описывающие динамику изменения состояния подвижного объекта. Что конкретно они могут описывать? Они могут описывать динамику изменения угловых и/или траекторных координат как реакцию на возмущающие или управляющие воздействия в правой части соответствующих уравнений. Значение координат подвижного объекта на траектории ОБЪЕКТИВНО является случайным процессом (случайной функцией времени). Этот факт учитывается в математических моделях подвижных объектов в виде задания случайных функций времени (по физическому смыслу это траекторные возмущения и/или управления) в правой части соответствующих дифференциальных (разностных) уравнений динамики. Решением указанных дифференциальных уравнений с правой частью являются случайные процессы изменения координат подвижного объекта на траектории.


Таким образом, дифференциальные (разностные) уравнения являются математическими моделями динамических систем и их решения описывают СЛУЧАЙНЫЕ ПРОЦЕССЫ.
В рамках корреляционной теории случайных процессов и применительно к линейным дифференциальным (разностным) уравнениям, УСТАНОВЛЕНЫ СВЯЗИ между структурой, порядком и коэффициентами дифференциальных (разностных) уравнений, в правой части которых присутствует случайный процесс белого шума – с одной стороны, и структурой и параметрами КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ решений указанных уравнений – с другой стороны. Например, дифференциальные уравнения 1-го и 2-го порядка, описывают случайные процессы с корреляционными функциями следующих видов:
Дифференциальное уравнение 1-го порядка:
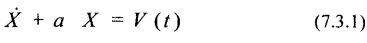
описывает случайный процесс с корреляционной функцией вида:

в зависимости от корней своего характеристического уравнения имеет различные типы корреляционных функций своих решений. Например, в случае комплексно-сопряжённых корней характеристического уравнения соответствующая корреляционная функция решения дифференциального уравнения (7.3.3) будет иметь вид:
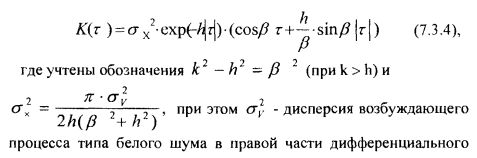

Для линейных дифференциальных (разностных) уравнений более высокого порядка (выше 2-го), аналитические связи между коэффициентами дифференциальных (разностных) уравнений и структурой и параметрами корреляционных функций будут более сложными. Однако современная теория также позволяет установить указанные зависимости.
Отметим далее, что дифференциальные (разностные) уравнения, возбуждаемые на входе (т. е. в правой части) случайными процессами типа белого шума и генерирующие на выходе статистически окрашенный случайный процесс, являющийся решением указанных уравнений, называются ФОРМИРУЮЩИМИ ФИЛЬТРАМИ.
В концептуальном плане наличие однозначного соответствия между дифференциальными (разностными) уравнениями с одной стороны, и статистическими свойствами генерируемых ими случайных процессов – с другой стороны, является чрезвычайно важным.
Указанное соответствие открывает путь построения модели функционирования финансового рынка, как стохастической дифференциальной системы. Математической моделью подобной системы могут служить формирующие фильтры в виде дифференциальные и разностных уравнений.
С математической точки зрения модели функционирования финансового рынка (формирующие фильтры) и модели технических динамических систем (дифференциальные уравнения) будут совершенно одинаковыми по своей форме.
Именно это последнее обстоятельство позволяет распространить для финансового рынка мощные математические методы оптимального управления, развитые применительно к техническим динамическим системам.
|