2.5. Диверсификация Марковица
Множество недоминируемых портфелей, называемое эффективной границей, может быть построено решением общей задачи минимизации риска, впервые рассмотренной Марковицем:
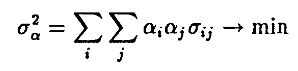
при двух ограничениях. Первое ограничение фиксирует желаемый уровень доходности, а второе ограничение нормирует весовые коэффициенты портфеля (без ограничений на короткую позицию):
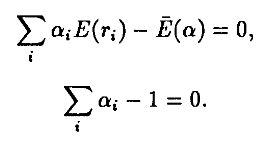
Целевая функция Лагранжа для задачи минимизации риска при фиксированном уровне доходности записывается так:
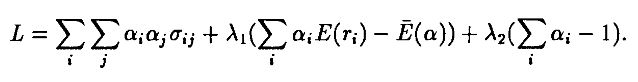


Портфель, минимизирующий риск, находится, если положить ∂L/∂αi = ∂L/∂λj = 0 для всех акций i и для j = 1,2. Эти условия первого порядка определяют систему уравнений, линейную по весовым коэффициентам портфеля и множителям Лагранжа и потому решаемую с помощью матричных методов (с возможностью использования стандартных пакетов). Например, целевая функция для задачи с тремя типами акций записывается так:

Условия первого порядка для данной задачи
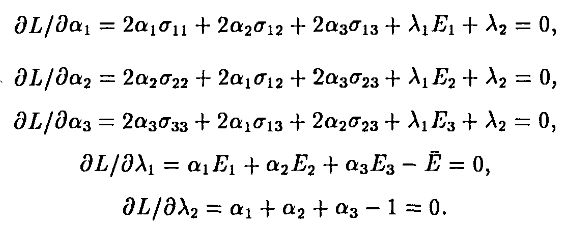
В матричной форме
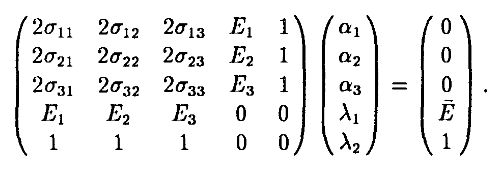
Если обозначить матрицу “риск–доходность” через V, вектор (α, λ) через A и вектор в правой части через W, то мы должны решить относительно А систему уравнений
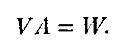
Инвертируя матрицу “риск–доходность”, получим решение:
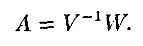
Данное решение определяет оптимальный портфель из акций трех типов, реализующий требуемую доходность (при минимальной дисперсии). Варьируя желаемую доходность, можно построить всю эффективную границу. Заметим, что для определения эффективной границы как функции Е достаточно двух последних столбцов матрицы V-1, поскольку первые три компоненты вектора W равны нулю. Это иллюстрируется следующим примером.
Пример
Рассмотрим три рисковые ценные бумаги, характеризующиеся следующими рисками и доходностью:

При данной информации матрица V равна

а вектор W равен
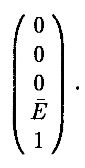
Обратная матрица для V равна

Умножая W на V-1 спереди, получим общее решение задачи минимизации дисперсии портфеля как функции Е для акций 1, 2 и 3:
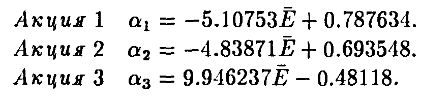
Например, если мы хотим получить ожидаемую доходность .1 (т. е. 10%), мы должны подставить .1 вместо Е в приведенные выше формулы минимизирующих дисперсию весовых коэффициентов:

|