2.7. Добавление безрисковых активов

Предположим теперь, что имеется безрисковый актив с доходностью r_f. Это соответствует точке на оси Y, поскольку безрисковый актив, по определению, имеет нулевую дисперсию.

Наличие безрисковых активов меняет открытые перед нами инвестиционные возможности, поскольку мы можем комбинировать его с рисковыми активами. Фактически меняется эффективная граница инвестиционных возможностей. Проиллюстрируем это положение, используя следующий рисунок:

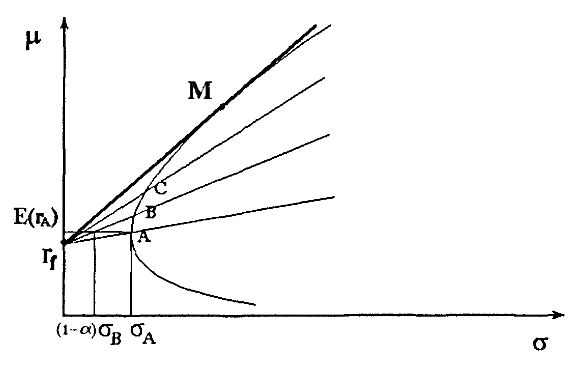
Рассмотрим точку типа A, которая соответствует портфелю с ожидаемой доходностью Е(r_A) и стандартным отклонением σ_A. Но мы можем получить ту же самую ожидаемую доходность, но с меньшей дисперсией, составив комбинацию портфеля точки В с безрисковым активом. Если мы инвестируем а в r_f и (1 – α) в B, то ожидаемая доходность будет αr_f + (1 – α)E(r_B), а стандартное отклонение (1 – α)σ_B. Выбрав α подходящим образом, как показано на рисунке, мы получим ту же самую ожидаемую доходность с меньшим риском.

Продолжая в том же духе (рассмотрев, например, точку G), мы обнаружим, что самое лучшее, что мы можем сделать, это составить комбинацию из безрискового актива и точки М на рисунке. Это приводит к следующей эффективной границе:

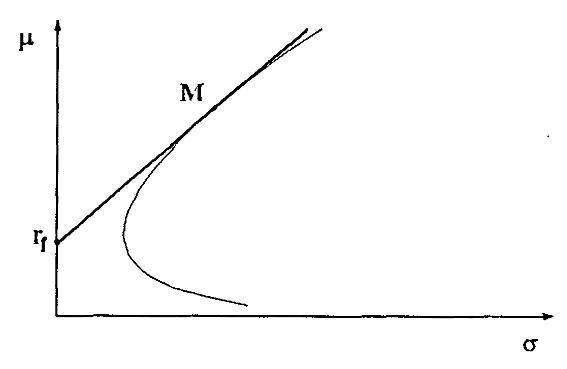
Точка M называется рыночным портфелем (market portfolio). Эффективная граница превратилась в прямую, проходящую из r_f через М, и любой инвестор с предпочтениями, определенными выше, будет выбирать портфель так, чтобы ожидаемая доходность и стандартное отклонение лежали бы па этой прямой. Эта прямая часто называется Capital Market Line (CML). Заметим, что эта прямая касается “пули” в точке М. Пусть Е(r_M) и σ_M – ожидаемая доходность и стандартное отклонение в точке М. Наклон прямой тогда равен

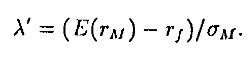
Это число показывает, какой долей ожидаемой доходности мы должны пожертвовать, чтобы уменьшить риск, и говорит об имеющихся возможностях компромисса между риском и доходностью. Иногда эту величину называют рыночной ценой риска.

Каждый раз, когда заданы цены всех акций на рынке, тем самым определены и все возможности для компромисса между риском и доходностью. Инвесторы торгуют на рынке и формируют портфели. Равновесие наблюдается, если цены на акции таковы, что ни один из инвесторов не захочет изменить свой портфель и предложение активов (как рисковых, так и безрисковых) равно спросу. Это условие определяет равновесную рыночную цену риска. Если рыночная цена риска известна, мы можем определить ожидаемую доходность или эквивалентно цены на все рисковые активы.

Это делается следующим образом. Предположим, рассматривается возможность инвестирования доли θ всего капитала в акции i и доли (1 – θ) в М. Это приведет к следующей диаграмме (как функции θ):

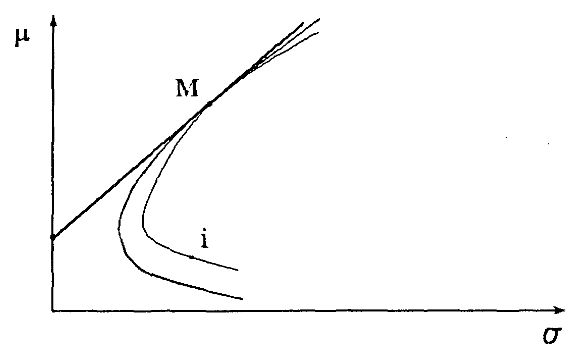
Заметим, что внутренняя линия касается внешней границы “пули” в точке М, поскольку лежит целиком внутри внешней и проходит через М.

Ожидаемая доходность равна

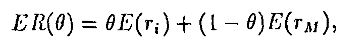
а стандартное отклонение

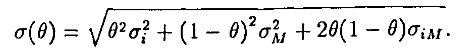
Мы можем вычислить, как ожидаемая доходность и дисперсия зависят от параметра θ. Если продифференцировать каждое из выражений по θ, мы получим

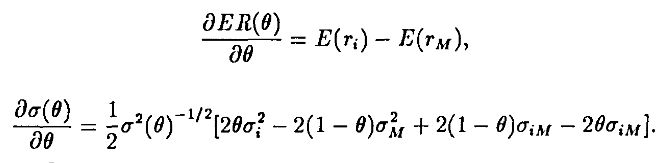
Отношение этих двух производных, вычисленное в точке θ = 0, даст наклон внутренней линии в точке М. Поскольку эта внутренняя “пуля” касается внешней “пули” в точке М, то она касается в точке М и прямой, проходящей из r_f через М. Отсюда получаем:

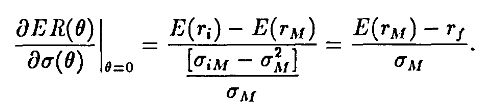
Решая это уравнение, получим

Коэффициент β_i = σ_iM/σ²_M называется “бета” актива i.

Приведенное уравнение определяет Security Market Line (SML). Это уравнение говорит, что в равновесии ожидаемая доходность Е(r_i) актива i связана с ожидаемой доходностью рыночного портфеля Е(r_M) через цену риска, λ' = (E(r_M) – r_f)/σ_M, задающую наклон прямой CML. Выражение в квадратных скобках есть превышение ожидаемой доходности рыночного портфеля над безрисковой доходностью. Модель определения цен основных активов (САРМ) говорит, что избыточная доходность актива i (равная E(r_i) – r_f) должна быть пропорциональна избыточной доходности рыночного портфеля, где коэффициентом пропорциональности служит “бета” актива.

В терминах рыночной цены риска уравнение SML переписывается следующим образом:

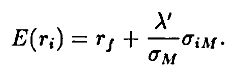
В такой записи SML в равновесии есть функция, линейная по ковариации актива с рыночным портфелем и по “рыночной цене риска”, определяемой в этом случае как

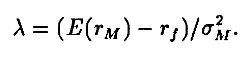
Содержание

Далее