2.10. Равновесный анализ формирования цен в условиях неопределенности

Формулировка, которую мы примем, слегка отличается от той, что рассматривалась ранее. Мы предполагаем, что инвесторы избегают риска и интересуются размером капитала на конец периода. Капиталы в начале периода считаются заданными. Выплаты по ценным бумагам, в которые можно инвестировать капитал, являются стохастическими, и мы снова предполагаем, что конкретные выплаты в конце периода будут зависеть от реализованного состояния мира. Инвесторы могут формировать портфели рисковых активов, и следовательно, финальные выплаты будут зависеть от состояния мира. Мы предполагаем, что инвесторы оценивают портфель по величине ожидаемой полезности (см. приложение). Мы сделаем более специфическое допущение относительно предпочтений инвесторов, а именно, предположим их квадратичными.

Следствием такого допущения является то, что инвесторы интересуются только ожидаемой доходностью и дисперсией, но не другими характеристиками своего портфеля.

Инвесторы будут формировать портфель так, чтобы максимизировать ожидаемую полезность при ограничениях по начальному капиталу и по предложению бумаг на рынке. В условиях конкурентного рынка установление равновесных цен на финансовые активы означает, что:

1. Инвесторы формируют портфели, максимизирующие ожидаемую полезность.

2. Предложение активов каждого вида равно спросу.

Конкурентное равновесие в экономике с неопределенностью строится следующим образом.

Во-первых, при данных ценах мы докажем справедливость теоремы об инвестировании в два фонда. Во-вторых, мы определим равновесную стоимость каждой фирмы в экономике. После этого легко подсчитываются равновесные цены на каждую акцию.

Напомним, что если инвесторы интересуются только ожидаемой доходностью и дисперсией доходности портфеля, то они будут формировать свой портфель как комбинацию только рыночного портфеля M и безрискового актива. Одним из следствий этого результата является факт, что доля стоимости фирмы г, принадлежащая инвестору k, равна доле фирмы j. Пусть V_i и V_j обозначают рыночные стоимости этих фирм, а z_i^k и z_j^k – доли стоимостей, принадлежащих инвестору k, так что количество денег, вложенных инвестором k в фирму i, равно z_i^kV_i. Тогда легко получить равенство z_i^k = z_j^k. Напомним, что Y^k обозначает количество денег, вложенных инвестором k в рисковые активы, и m_i обозначает долю фирмы i в рыночном портфеле. Тогда стоимость фирмы i в портфеле инвестора k равна m_iY^k. Таким образом, мы имеем z_i^kV_i = m_iY^k, так что условие z_i^k = z_j^k будет выполнено, если m_iY^k/V_i = m_jY^k/V_j, или m_i/V_i = m_j/V_j. Но последнее равенство следует непосредственно из определения m_i и m_j. Поскольку m_i = V_i/V, где V – суммарная рыночная стоимость всех фирм, мы получаем m_i/V_i = 1/V = m_j/V_j.

Для аналитического удобства спрос каждого инвестора задается как желаемая (для владения) доля каждой фирмы. Мы покажем, что из предположения о квадратичности функций полезности вытекает, что каждый инвестор желает владеть одной и той же долей во всех фирмах. Этот факт существенно используется при выводе основного уравнения для рыночной стоимости фирмы. Оказывается, что стоимость каждой фирмы может рассматриваться как текущая стоимость ее будущих доходов, “скорректированных с учетом риска”.

Обозначения и допущения

Построение равновесия

Капитал инвестора k в состоянии s (в конце периода) оценивается формулой

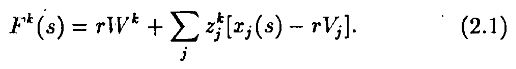
В этом выражении rW^k определяет доход от начального капитала, –z_j^krV_j есть потери дохода из-за вложения капитала в фирму j, наконец z_j^kx_j(s) есть выплаты фирмы j инвестору k.

Ожидаемая полезность конечного капитала, заданного формулой (2.1), в случае квадратичной функции равна

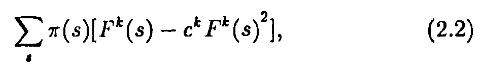
и, если нет ограничений на короткую позицию, необходимое и достаточное условие для максимизации ожидаемой полезности по переменным z_j^k записывается

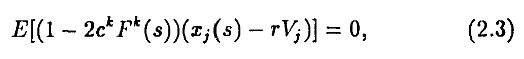
где Е обозначает математическое ожидание выражения в квадратных скобках.

Можно вывести следующие соотношения:

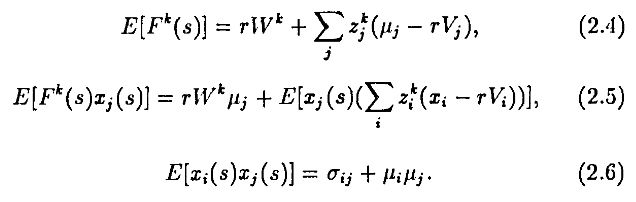
Раскрывая (2.3) и используя (2.4)–(2.6), можно записать условия первого порядка по отношению к z_j^k в следующем виде:

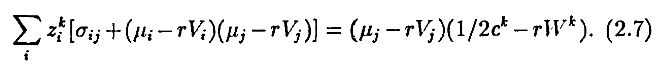
Отметим, что характеристики инвесторов входят в правую часть множителем. Поэтому можно решить соответствующую систему относительно вспомогательных переменных z_j, умножив которые затем на (1 / 2c^k – rW^k), мы получим искомые переменные z_j^k. Теорема об инвестировании в два фонда, в сущности, основана на возможности представить уравнение в такой форме. Окончательно, пусть z_j* – решение следующей системы:

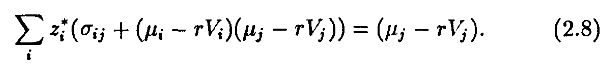
Тогда z_j^k определяется уравнением

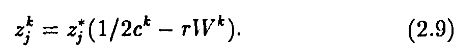
В равновесии должно выполняться условие Σ_kz_j^k = 1, т.е. сумма долей любой из фирм по всем инвесторам должна равняться единице. Отсюда мы имеем

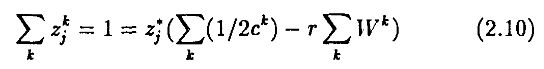
и, тем самым,

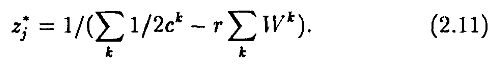
Из (2.10) и (2.11) следует

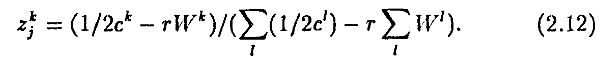
Из (2.12) видно, что z_j^k не зависит от j, так что доля любой фирмы для инвестора k определяется только характеристиками инвестора. Эту долю обозначим через z^k.

Используя данный результат, становится относительно легко определить V_j – рыночную стоимость фирмы j. Уравнение спроса (2.7) можно теперь переписать в виде

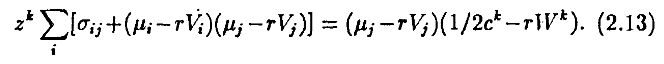
Поскольку Σ_kz^k = 1, мы имеем

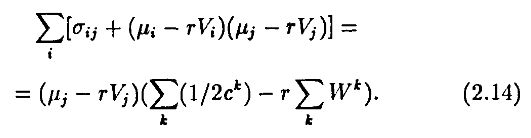
Наконец, используем тот факт, что Σ_iV_i = Σ_kW^k, т.е. суммарная рыночная стоимость всех активов равна суммарному капиталу в экономике. Подставляя в (2.14), получаем

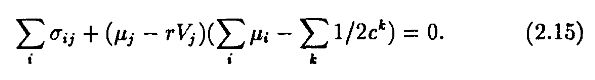
Раскрывая, получаем

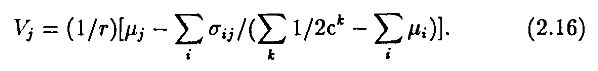
Уравнение (2.16) определяет рыночную стоимость фирмы в целом. Уравнение утверждает, что стоимость фирмы j равна текущей стоимости (по проценту безрискового актива) скорректированных с учетом риска ожидаемых платежей. Поправка на риск зависит от среднего отношения инвесторов к риску и от ковариаций платежей данной фирмы со всеми другими фирмами в экономике (систематический риск).

Содержание

Далее