3.4. Биномиальная модель цены: европейский однопериодный колл-опцион
Биномиальная модель (binomial option pricing model) предполагает, что в любом периоде цена акции может сместиться либо вверх, либо вниз от текущей цены. Пусть u > 1 – сдвиг вверх, a d < 1 – сдвиг вниз. В рамках использовавшихся нами обозначений: высокая цена Su = Su, низкая цена Sd = Sd, где S есть текущая цена акции. Как и ранее, при определении цены опциона нам не потребуются вероятностные предположения об изменении цены акции.
Мы будем использовать следующие обозначения:
S = текущая цена акции;
Su = будущая высокая цена акции (состояние H);
Sd = будущая низкая цена акции (состояние L);
r = 1 + безрисковый процент;
X = цена исполнения;
С – цена колл-опциона, которую и надо определить.
Важно: актуальная возможность выиграть $40–$250 реальных (не бонусных) средств в конкурсе на демо-счетах.
Будем предполагать, что u > r > d, – это необходимо для предотвращения арбитража (если r > u, то надо продать акции и инвестировать вырученную сумму под безрисковый процент r; если d > r, то надо занять деньги под безрисковый процент r и купить акцию). Определим
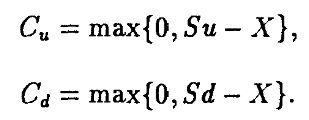
Если и Сu, и Cd равны нулю, то колл-опцион заведомо не будет исполняться, так что предположим, что Сu > 0.
А) Рассмотрим портфель из +1 акции и –k колл-опционов. Будущие платежи от этого портфеля составят:
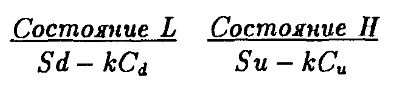
Выберем k так, чтобы
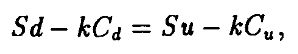
т. е. получился безрисковый портфель. Для этого необходимо, чтобы
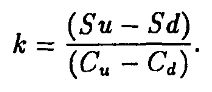
Это отношение называется коэффициентом полного хеджирования (hedge ratio).
Стоимость приобретения такого портфеля в настоящий момент есть S – kC. Так как портфель дает гарантированный доход Su – kСu, должно быть выполнено соотношение
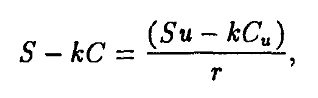
откуда
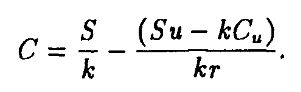
Цена колл-опциона С есть функция текущей цены акции, будущих возможных цен акции, цены исполнения опциона (от которой зависят Сu и Cd) и безрискового процента.
В нашем примере было X = 30, Su = 40, Sd = 20, r = 1, так что
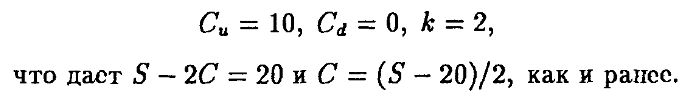
Б) Мы можем также определить цену опциона, используя акции и безрисковые активы для воспроизведения платежей, порождаемых опционом. Пусть мы покупаем ∂ акций и занимаем $6. Мы хотим выбрать ∂ и b так, чтобы
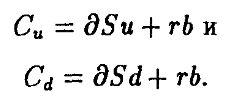
Из этих двух уравнений следует, что ∂ и b должны быть:
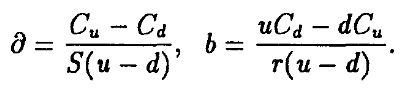
Если мы выбираем ∂ и b в соответствии с этими уравнениями, то наш портфель из ∂ акций и $b безрисковых активов порождает те же самые платежи, что и колл-опцион. Но тогда цена колл-опциона должна равняться цене (эквивалентного) портфеля, иначе можно было бы получить чистую арбитражную прибыль. Это означает, что цена опциона есть
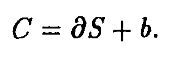
Подставляя данные из рассмотренного выше примера, мы снова получим С = (S – 20)/2.
Это уравнение имеет вид линейной зависимости между S и С, так что ∂ можно рассматривать как производную от С по S, т. е. как меру чувствительности цены колл-опциона на акцию по отношению к цене этой акции. Эта величина обычно называется “дельтой” опциона. Ясно, что ∂ = 1/k, где k – коэффициент полного хеджирования.
Аналогичная зависимость выводится и для европейского пут-опциона. Требуя, чтобы
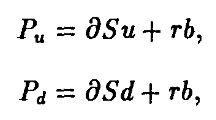
получим, что
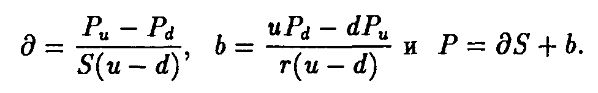
Заметим, что дельта пут-опциона отрицательна, так как Рu < Рd.
|
