3.7. О нейтральной к риску оценке

Как мы уже видели, для вычисления цены европейского колл- опциона можно использовать портфель из акций и безрисковых активов, воспроизводящий поток платежей от опциона. Из соотношений

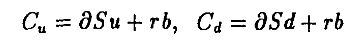
мы получили, что

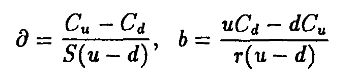
и цена колл-опциона С = ∂S + b. Подставляя d и b, получим:

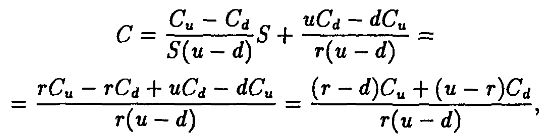
T. e.

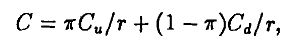
где

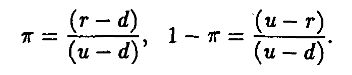
Так как u > r > d, то 0 < π < 1, так что π можно трактовать как вероятность. Тогда, согласно полученному выражению, цена колл-опциона есть средняя будущая цена опциона, дисконтированная на безрисковый процент, а среднее значение подсчитывается на основе вероятности появления цены акции, равной Su.

Отсюда следует, что если мы имеем нейтрального к риску субъекта, который считает, что колл-опцион будет стоить С_u с вероятностью π и C_d с вероятностью (1 – π), то этот субъект будет вычислять текущую цену опциона с полном соответствии с выведенным нами уравнением. Заметим, что мы нигде не предполагали наличия априорных вероятностей появления той или иной цены акции и, соответственно, будущей оценки опциона. Изложенный подход называется нейтральной к риску оценкой.

“Вероятность” х допускает и другую интерпретацию, связанную с ценой акции. Заметим, что

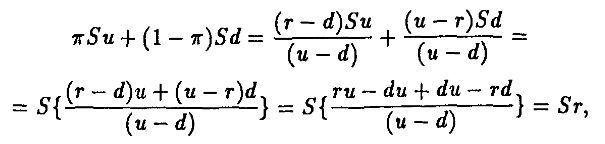
так что

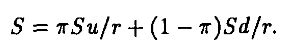
Другими словами, только вероятность π совместима с гипотезой нейтральности к риску инвесторов при данных текущей цене S и возможных будущих ценах Su и Sd, а также коэффициенте дисконтирования r. Поэтому π можно назвать “нейтральной к риску вероятностью”.

Еще раз подчеркнем, что в наших начальных предположениях не было ни вероятностей, ни рассчитывающих на средний доход инвесторов, ни самого понятия среднего дохода. Мы всего лишь воспроизвели поток платежей от колл-опциона с использованием финансовых инструментов – акций и безрискового актива, цены на которые предполагались известными (r – цена кредита, Su, Sd – цены на акции). Но наш подход работает лишь тогда, когда возможно воспроизведение. Если бы такое воспроизведение оказалось невозможным, мы бы ничего не смогли сделать.

Каким образом можно согласовать нейтральную к риску оценку с моделью определения цены на фонды, такой как САРМ, в которой для оценки активов приходится решать сложные задачи? Ответ заключается в том, что весь риск, связанный с обладанием опционом, может быть устранен с помощью акций и (безрисковых) облигаций. Эта возможность и лежит в основе принципа нейтральной к риску оценки.

Этот принцип, применимый, в частности, к биномиальным моделям событий, в других случаях требует модификации. Пусть, например, цена акции к концу периода может не только повышаться до Su и понижаться до Sd, но и оставаться постоянной на уровне 5. Рассмотрим однопериодный колл-опцион, и пусть цена исполнения X отвечает условиям Sd < X < S < Su. Платежи по опциону будут Su – X, Sd – X и 0. Если мы хотим воспроизвести их посредством п акций и m безрисковых облигаций, мы должны выполнить условия (здесь B – цена безрисковой облигации в начале периода):

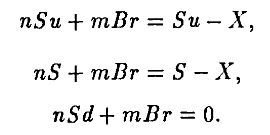
Эта система из трех уравнений с двумя неизвестными (n и m) решения не имеет. Таким образом, только при помощи акций и облигаций нельзя полностью устранить риск от опциона. Это можно было бы сделать лишь при наличии третьей, “независимой” от первых двух, ценной бумаги.

В рамках многопериодной биномиальной модели можно определить цену опциона и тогда, когда число возможных конечных значений цены акции больше двух. Если, например, в двухпериодной модели положить u = 1/d, то два из четырех возможных конечных значений цены сольются, Sud = Sdu = S; если дополнительно предположить, что Sdd < X < S < Suu, то возникает задача с тремя состояниями, которая не может иметь решения в рамках биномиальной модели. Тем не менее решение есть даже в более общем случае, когда u ≠ 1/d. В чем же здесь дело?

Дело в возможности продолжить торговлю после первого периода. Мы не обязаны сохранять наш портфель неизменным во втором периоде и можем его изменить. Собственно, мы уже видели в предыдущем разделе, что коэффициент полного хеджирования изменяется от периода к периоду.

Итак, пусть n_u, n_d, т_u, m_d разрешают систему уравнений:

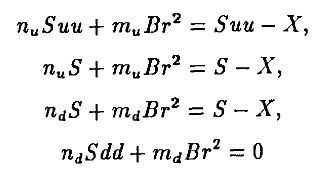
(индексы и и d соответствуют двум состояниям, II и L, на конец первого периода). Отсюда цены опционов для каждого из состояний суть

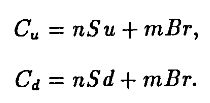
Теперь осталось найти пятна первый период из системы

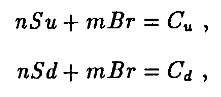
что позволит определить текущую цену опциона:

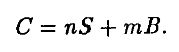
Возможность продолжать торговлю, т. е. изменять портфель при переходе от периода к периоду, как бы “увеличивает” количество имеющихся в нашем распоряжении ценных бумаг.

Кроме оценки опциона мы можем применить данный подход к задаче хеджирования (ограничения) риска. Пример – динамическое хеджирование портфеля ценных бумаг. Пусть мы управляем портфелем ценных бумаг и хотим застраховаться от падения стоимости этого портфеля ниже определенной величины, например, X, через три месяца. Простейший способ – это купить пут-опцион на этот портфель с ценой исполнения X и сроком погашения три месяца. Пусть, однако, торговля такими опционами не производится. Если цена портфеля изменяется согласно биномиальной модели (либо согласно обсуждаемой ниже логнормальной модели), то можно воспроизвести пут-опцион посредством достаточно частой (в пределе – непрерывной) торговли, создавая тем самым искусственный опцион на этот портфель. Разумеется, при слишком активной торговле мы столкнемся со значительными транзакционными издержками, так что в реальности точное воспроизведение требуемого пут-опциона невозможно.

Содержание

Далее