1. Временна́я структура процентных ставок

Долговые контракты (например, облигации – bonds) относятся к наиболее важным финансовым активам. Долговой контракт характеризуется

1) номинальной стоимостью;

2) сроком погашения;

3) купоном или процентными выплатами, которые будут производиться на протяжении срока действия контракта.

Самыми распространенными долговыми контрактами являются государственные облигации. Например, тридцатилетние казначейские облигации имеют номинальную стоимость от $10 000 до $1 000 000 и различные купонные ставки. По ним выплачиваются проценты каждые полгода. Если такая облигация имеет номинальную стоимость $10 000 и купонную ставку 10%, то по облигации будет выплачиваться $500(= 10 000 х 0.1/2) каждые шесть месяцев (мы делим 10% на 2, так как 10% – годовая процентная ставка), а также будет выплачена номинальная стоимость $10 000 в конце 30-летнего периода.

Другой важный тип облигаций – это бескупонные облигации (zero-coupon bond), по которым не производятся купонные платежи, а выплачивается только номинальная стоимость в момент погашения (например, казначейские вексели).

Наша цель – определить стоимость облигации, т. е. цену, по которой следует ею торговать. Давайте начнем с изучения бескупонной, или дисконтной, облигации, по которой выплачивается номинальная стоимость Р в следующем периоде. Предположим, облигация имеет цену Р. Если r – процентная ставка (interest rate) за один период, тогда должно быть выполнено равенство:

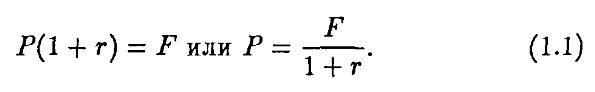
Чтобы доказать это, предположим от противного, что Р(1 + r) < F. Тогда мы займем $Р под процент r и купим облигацию. В следующем периоде мы будем должны уже Р(1 + r), но получим за облигацию F > Р(1 + r), т. е. получим чистый арбитражный выигрыш. Поэтому остается предположить, что Р(1 + r) > F. Однако, если Р(1 + r) > F, мы продадим облигацию и инвестируем деньги под процент г. В следующем периоде мы будем должны F (так как обязаны выплатить номинальную стоимость облигации), но инвестиции принесут нам Р(1 + r) > F. Отсюда Р(1 + r) ≤ F. Поскольку ранее мы получили, что Р(1 + r) ≥ Р, формула доказана:

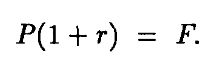
Теперь предположим, что мы знаем цену облигации – Р, ее номинальную стоимость – Р и срок погашения – конец первого периода. Какова тогда подразумеваемая процентная ставка? Эта процентная ставка, называемая доходностью (yield), равна доходу от облигации, выраженному в процентах. Для любой ценной бумаги такой доход равен будущей цене, деленной на текущую, минус 1. В нашем случае будущая цена равна номиналу, т. е. F. Текущая цена равна Р, поэтому доходность равна

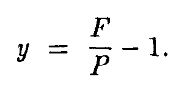
Заметим, что процентная ставка на один период должна быть равна доходности, иначе появится возможность арбитража (arbitrage opportunity). Такая возможность возникает, когда можно получить гарантированный (безрисковый) доход без каких-либо инвестиций. В нашем случае предположим, что процентная ставка при займе на один период равна г, а доходность нашей облигации равна y > r. Тогда мы займем деньги под процент r и купим облигацию. Если y < r, то мы продадим облигацию и инвестируем их под процент r.

В случае облигации на два периода (с выплатой номинальной стоимости F в конце второго периода) нам нужно знать процентную ставку на два периода. Или наоборот, мы можем вычислить доходность облигации к погашению (yield to maturity), исходя из цены на такую облигацию, т. с. вычислить r₂ из уравнения:

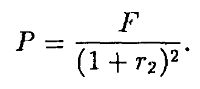
При рассмотрении широкого диапазона сроков погашения нужная информация содержится в кривой доходности (yield curve), показывающей зависимость доходности к погашению от срока погашения облигации. Взаимоотношение между доходностью долговых контрактов и сроком погашения называется временной структурой процентных ставок (term structure of interest rates) или кривой доходности. Практически эта кривая строится по текущим рыночным ценам на государственные долговые обязательства (которые признаются безрисковыми – risk-free asset) различных сроков погашения. (Получаемые процентные ставки – безрисковые – risk-free interest rates.) Отметим, что цена облигации и соответствующая процентная ставка (доходность) взаимозаменяемы: если известно одно, всегда можно вычислить другое. Обычно предполагается, что кривая доходности имеет наклон вверх. Это значит, что доходность к погашению возрастает с ростом времени погашения. Если r_t обозначает доходность t-периодной бескупонной облигации, то r_t > r_τ для t > τ. Фактически отмечались весьма разнообразные формы кривой доходности. Имеется несколько теорий, пытающихся объяснить временную структуру процентных ставок, в том числе базирующихся на концепциях ожиданий и предпочтения ликвидности.

Если известна временная структура процентных ставок, то несложно определить цену других долговых контрактов, таких как купонная облигация. Вообще, если мы знаем процентную ставку, по которой следует дисконтировать будущие платежи, мы можем вычислить цену любой последовательности платежей, развернутой во времени (потока платежей – cash flow). Наоборот, если известна цена облигации, то можно определить се доходность к погашению. Например, рассмотрим долговой контракт, по которому С_t выплачивается каждый период в течение Т периодов. Если Р – текущая рыночная стоимость этого контракта, то внутренняя доходность контракта равна процентной ставке r, удовлетворяющей равенству:

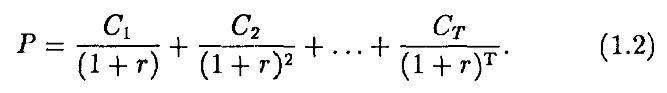
Пример

Рассмотрим бескупонную облигацию со сроком погашения 12 месяцев от данного момента и номинальной стоимостью $1000. Безрисковая процентная ставка на рынке на 12 месяцев равна 12%. Чему равна стоимость облигации?

Из уравнения (1.1) получаем, что стоимость бескупонной облигации равна

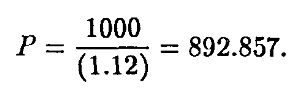
Если процентная ставка упадет до 10%, то стоимость облигации возрастет до $909.091.

Пример

Рассмотрим купонную облигацию с номинальной стоимостью $1000, ставкой 7% годовых, выплачиваемых ежемесячно, и сроком погашения 12 месяцев. В этом случае владелец облигации получает $5.83 каждый месяц и $1000 в конце года. Если текущая безрисковая процентная ставка – 1% в месяц, то стоимость облигации равна $953.1. Это можно проверить при помощи равенства (1.2), где С₁ = С₂ = ... = С₁₁ = $5.83, а С₁2 = $1005.83. Если текущая процентная ставка упадет до 5 – 6% в месяц, то стоимость облигации возрастет до $971.56.

Ординарной рентой называется поток платежей на Т периодов, при котором в каждый период выплачивается одна и та же сумма, т. е. С = С₁ = ... = C_t. Типичным примером ординарной ренты является закладная с фиксированной ставкой. В этом случае мы можем преобразовать формулу (1.2) следующим образом:

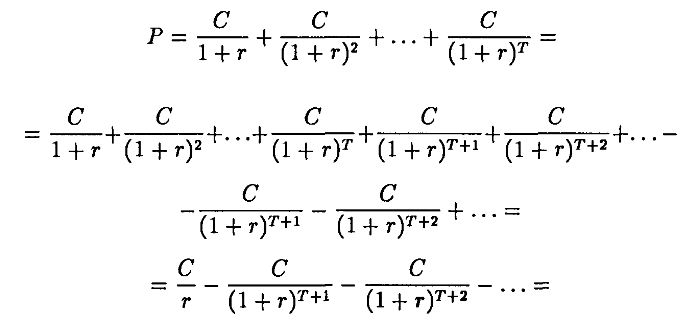
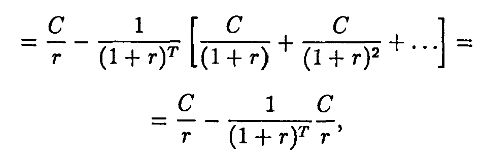
и получить формулу

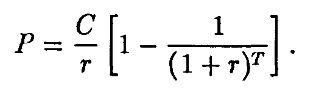
Эту формулу, называемую формулой ренты, как и раньше, можно применять двумя способами. Если известна процентная ставка, то с ее помощью можно вычислить цену (или текущую стоимость – present value) будущих платежей. Если же известна цена и будущий поток платежей, то по этой формуле можно вычислить процентную ставку, которая в этом случае называется доходностью.

При рассмотрении временной структуры становится ясно, что существует много различных процентных ставок. Чтобы не запутаться в них, будем использовать следующие обозначения. Символом _tr_T будем обозначать доходность к погашению в периоде t бескупонной облигации со сроком погашения в периоде Т. Текущим периодом всегда будет нулевой период. Таким образом ₀r_T будет обозначать сегодняшнюю доходность к погашению бескупонной облигации со сроком погашения в периоде Т. Если ₀r₁ и ₀r₂ известны, то определим ₁r₂ как решение уравнения:

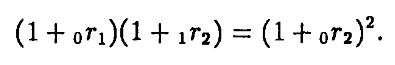
Величина ₁r₂ называется наведенной будущей процентной ставкой (implicit interest rate) или наведенной форвардной процентной ставкой (forward interest rate). Кривая доходности обычно показывает ставки типа ₀r₁ и ₀r₂. Наведенная форвардная ставка может быть вычислена через них. Вообще наведенной форвардной ставкой между периодами t и Т, вычисленной сегодня, называется величина _tr_T, удовлетворяющая уравнению:

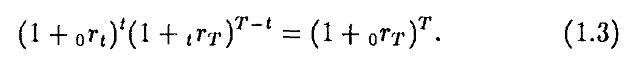
Если мы знаем доходность к погашению в любом периоде, мы можем вычислить цепу, или текущую стоимость, любого потока платежей. Таким образом, если ₀r_t является доходностью t-периодной бескупонной облигации и мы получаем платеж C_t в момент времени t, тогда

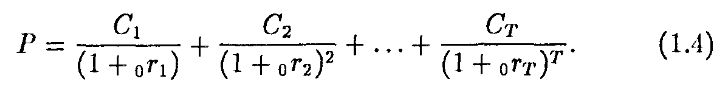
При расчете доходности к погашению нельзя забывать, что мы неявно исходим из предположения, что все денежные поступления каждый период реинвестируются под процент, соответствующий доходности, на оставшееся до погашения время. Чтобы доходность облигации реализовалась в виде реального дохода, нужно чтобы либо не было неопределенности в процентных ставках, либо облигация была бескупонной.

Рассмотрим купонный контракт, составленный как портфель (portfolio) бескупонных облигаций. Этот портфель сформирован так, чтобы платежи от Т бескупонных облигаций в точности соответствовали платежам купонной облигации. В этом случае каждая бескупонная облигация должна иметь собственный срок погашения так, чтобы были представлены все даты от 1 до Т. Пусть поток платежей такого портфеля соответствует платежам в уравнении (1.2) (C₁, C₂,... ,С_T). Текущая стоимость этих будущих платежей определяется текущими доходностями в соответствии с равенством (1.4). Уравнения (1.2) и (1.4) будут эквивалентны, если кривая доходности горизонтальна (т. е. текущая процентная ставка не зависит от времени до погашения). Эквивалентность предполагает, что купонные выплаты сразу реинвестируются под процент, соответствующий текущей доходности к погашению. В мире без неопределенности процентных ставок будущие значения доходности к погашению точно определены, и для держателя облигаций нет реинвестиционного риска (reinvestment risk). Однако на практике неопределенность процентных ставок имеет место, поэтому изменения доходности имеют стохастический характер и существует реинвестиционный риск.

Содержание

Далее