4.7. Рациональные ожидания с помехами

Цель данной теории – попытаться навести мост между наблюдаемыми явлениями и предсказаниями теории рациональных ожиданий. Рассматривается рынок ценных бумаг, на котором трейдеры формируют рациональные ожидания, однако равновесные цены не отражают всей наличной информации. И этих целях в теоретические построения включается потенциальный источник помех, который мешает ценам агрегировать информацию.

В изложении этой теории мы сосредоточим внимание на ожиданиях, использующих линейные правила прогнозирования. Следует заметить, что концепция равновесия при рациональных ожиданиях с помехами не налагает ограничений на источник помех. Любой источник помех, который разрушает статистическую достаточность цен по отношению к приватной информации трейдеров, приведет к аналогичному эффекту.

Условия

Пусть имеются один рисковый и один безрисковый актив, каждый сроком на один период.

Выплаты по рисковому активу в конце периода равны d ~ N(v, σ²), доходность безрискового актива равна r_f (можно полагать r_f = 1).

Источник неопределенности

Пусть S – фиксированное предложение акций на рынке. Рассматриваются два типа трейдеров. Одних приводит на рынок необходимость сберегать для будущего потребления, другие, обладая приватной информацией, рассчитывают на успешные спекуляции. Если объективная потребность в сбережениях стохастична, то и предложение на спекулятивном рынке стохастично. Например, пусть предложение акций фиксировано (= S), а потребность “вынужденных инвесторов” Ŝ_LC – нормально распределенная случайная величина. Тогда чистое предложение акций на спекулятивном рынке является нормально распределен ной случайной величиной (S – Ŝ_LC) = X_t(N). Стохастичность предложения служит существенным источником помех в рассматриваемой экономике.

Кроме того, предполагается, что суммарная дисперсия предложения будет расти с увеличением числа трейдеров, чтобы гарантировать, что этот источник помех не пропадет, когда количество спекулянтов станет достаточно большим (так что рынок окажется конкурентным).

В начале периода каждый трейдер-спекулянт получает некоторую приватную информацию yⁱ относительно выплат в конце периода по рисковым вкладам. Таким образом, yⁱ = d̂ + c_i, c_i ~ N(0, φ²).

Предположим, что потребность каждого трейдера в рисковых активах задастся линейной формулой

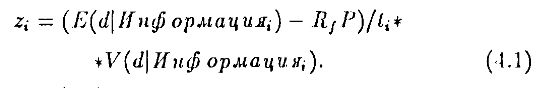
В уравнении (4.1) потребность является линейной функцией как цены, так и условного ожидания и условной дисперсии дивиденда на конец периода при заданной информированности. В результате, если трейдеры-спекулянты имеют одинаковые предпочтения, но различную информированность, то торговля будет обусловлена только различиями в информированности.

Помехи

В вышеописанных условиях способность цен агрегировать информацию существенно ослабляется стохастической составляющей спроса. Проблема в том, что трейдеры на рынке не могут отличить спекулянтов от вынужденных инвесторов. Высокая (низкая) цена может теперь возникать как за счет “хорошей” (“плохой”) информации, так и за счет высокого (низкого) спроса вынужденных инвесторов.

Ожидания

Ожидания воздействуют на условные среднее и дисперсию в уравнении (4.1) выше. Это, в свою очередь, влияет па цену, поскольку за счет цены выравниваются спрос и предложение.

Предположим, что трейдеры ограничиваются правилами прогнозирования, линейными по ценам и по приватной информации относительно ожидаемых дивидендов. В одном предельном случае, когда коэффициент перед ценой равен нулю, трейдер использует только приватную информацию. В другом предельном случае трейдер при выработке своих инвестиционных решений обращает внимание только на цены. Это можно интерпретировать так, что он абсолютно не интересуется никакой реальной информацией о фирме. Запишем такую форму правила прогнозирования в виде

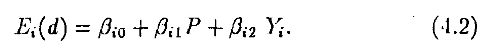
Полностью выявляющее равновесие и равновесие с помехами

Для построения (временного) равновесия подставим правило (4.2) в функцию спроса, просуммируем спрос и приравняем к суммарному предложению. Цены будут являться линейной функцией двух нормально распределенных случайных величин: предложения и взвешенного среднего всех приватных сигналов в Экономикс.

Отмстим, что для таких временных равновесий выполняются следующие условия:

1. Трейдеры максимизируют ожидаемую полезность капитала па конец периода при заданных правилах прогнозирования.

2. Спрос равен предложению.

Заметим, что существует континуум временных равновесий, поскольку для произвольно выбранных коэффициентов найдется цена, выравнивающая спрос и предложение. Если трейдеры не полностью игнорируют свои информационные состояния, то равновесная цена передает определенную информацию, поскольку в ней воплощены ожидания, основанные на индивидуальной информации. Таким образом, цена является источником информации, которая должна использоваться трейдерами на рынке. В равновесии при рациональных ожиданиях эта информация используется оптимальным образом, так что правила прогнозирования не являются произвольными. Так, в равновесии при рациональных ожиданиях должно удовлетворяться третье условие:

3. Для каждого трейдера прогноз должен подтверждаться реальной реализацией.

Условие 3 устанавливает, что если мы позволим каждому трейдеру пересматривать свои правила прогнозирования с использованием реализованных значений выплат по рисковым активам, то исходные правила прогнозирования не будут пересмотрены. Тем самым мы получим неподвижную (т. е. равновесную) точку в пространстве линейных правил прогнозирования.

Чтобы оцепить различие между полностью выявляющим равновесием и равновесием при рациональных ожиданиях с помехами, проанализируем смысл коэффициентов в оптимальном правиле прогнозирования. Если оптимальные весовые коэффициенты в уравнении (4.2) таковы, что β_i2 = 0 для каждого трейдера, то равновесие является полностью выявляющим равновесием в рациональных ожиданиях. С другой стороны, в равновесии при рациональных ожиданиях с помехами оптимальные веса β_i1 и β_i2 не равны нулю. Тем самым как цена, так и приватная информация являются существенными для принимаемых трейдерами решений. Б рассматриваемой постановке помехи, создаваемые стохастической компонентой спроса, гарантируют, что оба коэффициента окажутся ненулевыми.

Построение равновесия

Построим временное равновесие путем суммирования спроса (уравнение (4.1)) и приравнивания этой суммы реализованному предложению рисковых активов (т. е. X_t(N)). Исходя из этих условий получим равновесную цену как линейную функцию относительно d̂ и X_t(N). Итак,

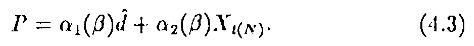
Заметим, что для любого множества начальных ожиданий рыночная равновесная цена является суммой двух нормально распределенных случайных величин. Коэффициенты в этой линейной функции являются, в свою очередь, функциями коэффициентов в правилах прогнозирования трейдеров, задаваемых уравнением (4.2) (Р – вектор коэффициентов). В этой экономике наблюдаемыми (ex ante или ex post) величинами являются случайные величины d, Р и γⁱ – все нормально распределенные со следующей ковариационной матрицей:

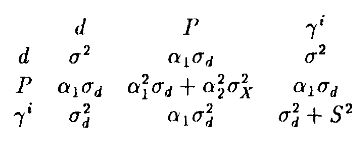
В данной линейной экономике оптимальные правила прогнозирования определяются с помощью метода наименьших квадратов. Из анализа вышеприведенной ковариационной матрицы и уравнения (4.3) следует, что элементы, включающие цены Р, являются функциями прогнозных весовых коэффициентов каждого трейдера. Таким образом, данные коэффициенты определяют цены ex ante, а с помощью метода наименьших квадратов мы можем вычислить отображение, определяющее пересчет каждым трейдером своих правил прогнозирования на основании информации, полученной по реализованным значениям d. Обозначим это отображение через M, так что М(β) = (М₀(β), M₁(β), М₂(β)). В равновесии при рациональных ожиданиях мы должны получить неподвижную точку: M(β^f) = (β^f₀, β^f₁, β^f₂), так что коэффициенты правил прогнозирования остаются неизменными при пересчете в свете реализованных состояний. Построение равновесия при рациональных ожиданиях с помехами как неподвижной точки такого отображения можно проиллюстрировать следующим образом.

На основании предыдущего отображение для пересчета М(β) вычисляется как сложная функция от α(β), непосредственно с помощью метода наименьших квадратов. Отсюда получаем (в предположении, что переменные понимаются как отклонения от их средних значений, так что β₀ = 0):

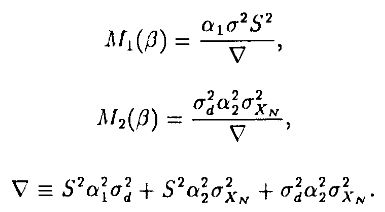
функции получены непосредственно из ковариационной матрицы; V есть детерминант подматрицы, заданной Р и γⁱ.

Отсюда можно получить следующий результат:

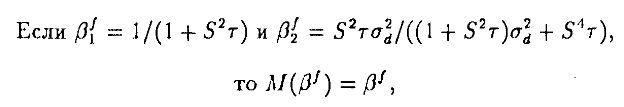
где lim_{N → ∞}σ²_Xt(N) / (N / r)² = τ > 0, так что дисперсия агрегированного предложения отделена от пуля в случае, когда экономика достаточно большая. Наконец, подставив равновесные весовые коэффициенты в уравнение (4.3), получим равновесную цену при рациональных ожиданиях с помехами.

Содержание

Далее