1.2. Процентный риск и форвардные контракты
Форвардный контракт является обязательством покупки или продажи какого-то (реального или финансового) актива в определенный момент в будущем и по оговоренной цене. Эта цена называется ценой поставки (delivery price) и устанавливается в момент заключения контракта. Однако поскольку никаких платежей в момент заключения контракта не производится, цена поставки устанавливается так, чтобы текущая стоимость форвардного контракта была равна нулю. В противном случае появилась бы возможность для арбитража, при которой либо продавец, либо покупатель бесплатно получил бы финансовый актив с положительной текущей стоимостью.
Это можно увидеть следующим образом. Пусть 0r1 обозначает процентную ставку на один период, 0r2 – на два периода, а f – форвардная цена двухпериодной бескупонной облигации с номинальной стоимостью F и поставкой в периоде 1. Тогда текущая цена облигации равна:
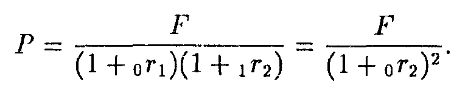
Мы утверждаем, что для предотвращения арбитража форвардная цена должна быть равна
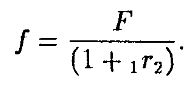


Для доказательства предположим, что f > F/(1 + 1r2). Тогда рассмотрим следующую стратегию: занять f/(1 + 0r1) на один период, использовать часть этой суммы для покупки бескупонной облигации и продать один форвардный контракт. Поскольку цена облигации строго меньше, чем f/(1 + 0r1), мы получим положительный платеж сегодня. В периоде 1 мы получим f, поставим нашу облигацию и вернем f, т. е. полностью закроем нашу позицию в периоде 1. При этом у нас останутся ранее полученные деньги, так что мы получили арбитражную прибыль. Если f < F/(1 + 1r2), тогда мы продадим облигацию в короткой позиции, инвестируем полученные деньги и купим форвардный контракт.
Это доказательство устанавливает, что стоимость форвардного контракта равна нулю, поскольку текущая стоимость поступающего потока платежей равна текущей стоимости уходящего потока. Если процентная ставка изменится, то изменятся и стоимость уже заключенных контрактов и форвардная цена на новые контракты.
Доказательство для многолетних контрактов несколько сложнее. Рассмотрим T-периодную бескупонную облигацию и форвардный контракт на поставку этой облигации в периоде 2, так что у поставленных облигаций останется (T – 2) периодов до погашения. Пусть текущая цена облигации равна Р, а f2 – форвардная цена. Мы хотим доказать, что f2 = Р(1 + 0r1)(1 + 1r2), т. е. форвардная цена равна стоимости облигации в периоде 2, наведенной текущей временной структурой. Это доказательство немного усложняется тем фактом, что если мы будем пытаться придерживаться той же стратегии, что и в однопериодном случае, то нам потребуется занять деньги на два периода под текущую двухпериодную процентную ставку. Нам нужно занять сумму
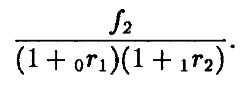
Если есть возможность занять эту сумму на два периода по наведенной доходности к погашению, т. е. процентной ставке, удовлетворяющей равенству (1 + 0r2)2 = (1 + 0r1)(l + 1r2), то мы сможем придерживаться той же стратегии, что и раньше. Если же такой возможности нет, то появится процентный риск и нам не обязательно удастся закрыть нашу позицию в периоде 2 без дополнительных затрат. Например, если мы займем под 0r1 сегодня, но столкнемся с изменившейся процентной ставкой при попытке продлить наш заем завтра, то можем понести потери, если, например, процентная ставка достаточно сильно возрастет.
Чтобы избежать этого, нужно занять на два периода под процент, определяемый сегодняшней временной структурой. Это достигается следующей стратегией: продаем двухпериодные облигации в таком количестве, чтобы их суммарная номинальная стоимость в периоде 2 была равна f2, и на полученные деньги покупаем Т-периодную облигацию. В периоде 2 мы поставляем облигацию, получаем f2, платим f2 по двухпериодным облигациям и закрываем нашу позицию. Легко проверить, что если f2 окажется больше, чем следует, то за продажу двухпериодных бескупонных облигаций мы получим больше, чем заплатим за Т-периодную облигацию.
С другой стороны, мы можем вычислить наведенную процентную ставку при одалживании (у кого-то/кому-то) денег на два периода. Одним из способов одалживания денег на два периода является покупка двухпериодной бескупонной облигации. Пусть 0r2 – двухпериодная процентная ставка при торговле этой облигацией такая, что
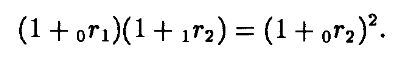
Другим способом такого займа является покупка Т-периодной облигации с Т > 2 и заключение на форвардном рынке сегодня контракта на продажу доходов от облигации в третьем и последующем периодах, т. е. контракт на поставку облигации в конце периода 2 по цене f2. Рассмотренное доказательство просто утверждает, что эти два вида займа должны принести одинаковые доходы.
Здесь мы использовали текущие и форвардные рынки для хеджирования процентного риска в периоде 2. Аналогичные рассуждения можно применить при хеджировании процентного риска в более общем виде. Например, вернемся к примеру с дюрацией. Имея обязательство выплатить L в периоде t, для хеджирования изменений в процентных ставках можно купить сегодня дисконтную облигацию с номинальной стоимостью L. Если же этого сделать нельзя, тогда альтернативой является покупка облигаций с более поздними сроками погашения и их форвардная продажа в момент времени t по известной цене, опять-таки избегая риска, связанного с изменением процентных ставок.
Конечно, если бы процентные ставки изменились, то изменилась бы и стоимость форвардного контракта. Главным различием между форвардными и фьючерсными контрактами (кроме того, что фьючерсные контракты стандартизованы и торгуются на биржах, в то время как форвардные контракты – на внебиржевых рынках) является то, что владелец фьючерсного контракта должен отслеживать на периодической основе (ежедневно либо еженедельно) рыночную стоимость своих фьючерсных позиций. Это означает, что если контракт имеет отрицательную стоимость, то короткая позиция (тот, кто поставляет данные активы в будущем) должна компенсировать разницу (или процент от нее) в деньгах. Если же стоимость положительна, то разницу должна компенсировать длинная позиция. Значит, процентный риск нельзя просто игнорировать, когда мы говорим о фьючерсных, а не о форвардных контрактах. Однако если нет неопределенности в динамике процентных ставок, то форвардные и фьючерсные контракты на один срок должны иметь одинаковые стоимости.
Во всех этих рассуждениях мы считали временную структуру данной и, исходя из этого, определяли цены форвардных контрактов. Однако можно считать данными цены на форвардные контракты, тогда цены на дисконтные облигации и процентные ставки вычисляются по ним. Таким образом, мы можем говорить о форвардной цене, определяющей форвардную процентную ставку (forward interest rate), и применять арбитражные рассуждения к процентным ставкам, получаемым при различных инвестиционных стратегиях.
Все это приводит нас к эквивалентному способу определения форвардной цены. Предположим, что мы можем положить деньги на депозит под 0r1 на один период и под 0r2 – на два периода, так что наведенная процентная ставка в следующем периоде 1 равна 1r2. Рассмотрим форвардное соглашение на депонирование $Х в периоде 1 на один период, и пусть 1i2 – форвардная процентная ставка на депозит, согласованная сегодня. Тогда по соглашению вы должны депонировать $X в периоде 1 на один период, а другая сторона – заплатить вам X(1 + 1i2) в периоде 2. В этом случае должно выполняться равенство:
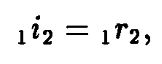
иначе существует возможность для арбитража. Например, если 1i2 > 1r2, то вы займете деньги на два периода под 0r2, депонируете их на один период под 0r1 и войдете в форвардное соглашение. В периоде 1 вы просто получите ваш депозит плюс процент и выполните форвардное соглашение. В периоде 2 вы получите больше денег, чем будете должны.
Из этих рассуждений не следует, что процентные ставки в следующем периоде будут равны наведенной форвардной ставке, и не следует даже, что вы ожидаете, что они будут равны. Фактически мы ничего не сказали о том, откуда взялись эти ставки! Мы обсудим это в следующем параграфе; сейчас мы лишь отметим, что временной структуре посвящены несколько теорий. В одной из них, “теории ожиданий”, утверждается, что наведенные будущие ставки равны ожидаемым будущим ставкам. Из этой теории следует, что инвесторы могут видеть, как рынок оценивает любую форвардную ставку. Практически было обнаружено, что временная структура содержит “премию за риск” так, что наведенные форвардные процентные ставки отличаются от ожидаемых рынком ставок. Аналогичный эффект наблюдается и для форвардных контрактов другого рода, например, для валют.
|