Следующий шаг
Основной недостаток формул [1.05-1.07] заключается в том, что они предполагают одинаковую вероятность реализации всех HPR. Поэтому нужна новая формула, которая допускала бы, чтобы с разными HPR ассоциировались различные вероятности. Такая формула позволила бы находить оптимальное f при условии, что дано описание распределение вероятностей HPR.
В 1992 г. я опубликовал набор формул, которые именно это и обеспечивали:

Откуда получаем относительный конечный капитал, или TWR:

или
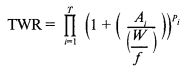


Наконец, если взять корень степени Σpi из уравнения [1.21], то получим средний прирост на игру, или среднее геометрическое HPR (оно будет играть важную роль в дальнейшем):

или
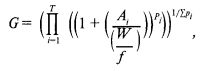

Точно так же, как вы могли пользоваться выражениями [1.04] для решения уравнений [1.03], уравнение [1.22] можно использовать для решения любых проблем с оптимальным f. Вместо формул [1.03-1.07] вы можете взять [1.22]. Для данных с распределением Бернулли это уравнение дает те же результаты, что и формулы Келли. Вы получите те же результаты, как и по формулам 1990 г., если подставите это распределение сделок (где вероятность каждой сделки равна 1/7) в [1.22]. Эту формулу можно использовать для максимизации ожидаемого значения логарифма любого начального количества чего угодно в условиях экспоненциального роста. Теперь посмотрим, как использовать эту формулу в контексте сценарного планирования.
|