7.2.3. Задача оптимального программного управления, как задача оптимизации в бесконечномерном пространстве

Задачи управления являются более общими, чем задачи оптимизации, так как их решением является функция времени U(t), а не точечное решение, как это имеет место в задачах оптимизации.

Покажем это на примере того, что задачу управления можно представить как задачу математического программирования (т. е. как задачу оптимизации) в бесконечномерном пространстве. Рассмотрим следующую задачу управления с целевым функционалом в форме Лагранжа:

Эта задача отличается от задачи оптимизации (7.2.1 – 7.2.5) следующими свойствами:

- она автономна, т.е. уравнения динамики (7.2.9) и целевой функционал (7.2.8) не зависят явно от времени;
- данная задача относится к классу задач Лагранжа, так как целевой функционал не зависит от конечного состояния или же от конечного момента времени;
- эта задача с закрепленным временем, т.к. t₁ задано, a X(t₁) произвольно;
- кроме того, полагается, что задача содержит только одну фазовую координату и один управляющий параметр.

Покажем далее, что задача управления эквивалентна задаче оптимизации в бесконечномерном пространстве.

где Δ – фиксированный положительный параметр. Пределом целевой функции (первое выражение в 7.2.15) при N, стремящимся к бесконечности, и Δ, стремящимся к нулю, при фиксированной величине NΔ = (t_i – t₀), является целевой функционал вида 7.2.8, т.е.:

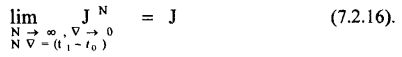
При переходе к пределу разностные уравнения (второе выражение в 7.2.15) превращаются в дифференциальные уравнения типа (7.2.9), а целевая функция со знаком суммирования (первое выражение в 7.2.15) превращается в интегральный целевой функционал вида (7.2.8).

Таким образом, задачу управления МОЖНО СЧИТАТЬ задачей математического программирования (оптимизации) в бесконечномерном пространстве. Этим пространством является множество всех кусочно-непрерывных вещественных функций U(t), определенных на промежутке t₀ ≤ t ≤ t₁.

С учетом сказанного, решение задач управления являются ничем иным, как динамической оптимизацией, обеспечивающей получение решения не в точке, а на множестве точек на интервале t₀ ≤ t ≤ t₁, т. е. решением указанной задачи является функция времени U(t).

Содержание

Далее