7.3.2. Математические модели финансового рынка в виде дифференциальных и разностных уравнений

Известно, что процесс функционирования финансового рынка имеет выраженную статистическую природу. В силу этого возможно проведение статистических исследований рынка, например, в рамках корреляционной теории случайных процессов.

Корреляционная теория случайных процессов позволяет описывать статистические свойства процессов с помощью моментных характеристик, главными из которых (применительно к скалярным случайным процессам) являются начальный момент 1-го порядка – математическое ожидание, центральный момент 2-го порядка – дисперсия, автоковариационная функция случайного процесса и взаимно-ковариационная функция между различными скалярными процессами. В случае гауссовского закона распределения случайного процесса указанные моментные характеристики полностью определяют его вероятностные свойства. Важность корреляционной теории состоит также в том, что все случайные процессы с той или иной степенью точности могут быть аппроксимированы через гауссовские процессы и, следовательно, выводы корреляционной теории будут справедливы для любых случайных процессов.

Таким образом, путь построения математических моделей случайных процессов, с которыми отождествляется статистическая динамика финансового рынка, может состоять в следующем:

- любыми известными статистическими методами необходимо получить оценки математических ожиданий, автоковариационных и взаимно-ковариационных функций для всех (или же наиболее значимых) инструментов финансового рынка;

- построить дифференциальные (разностные) уравнения, т.е. формирующие фильтры, генерирующие случайные процессы в соответствии с полученными оценками ковариационных функций.

Примечание. Теория и практика статистического исследования временных рядов показывает, что для построения их моделей достаточно ограничиться дифференциальными (разностными) уравнениями формирующих фильтров не выше 2-го порядка. Это означает, что определяются оценки корреляционных функций исследуемых случайных процессов, имеющих структуру типа (7.3.2, 7.3.4).

С учётом того, что поведение финансового рынка в динамике может быть описано с помощью дифференциальных (для дискретного времени – разностных) уравнений формирующих фильтров, возбуждаемых в правой части случайными процессами типа белого шума, приходим к тому, что модель финансового рынка в точности соответствует понятию стохастической дифференциальной системы.

Далее мы будем рассматривать только автономные стохастические дифференциальные системы, т. е. системы, коэффициенты дифференциальных (разностных) уравнений которых не зависят от времени.

Математическая модель финансового рынка в непрерывном времени

Математическая модель финансового рынка может быть представлена в виде векторно-матричного дифференциального уравнения вида:

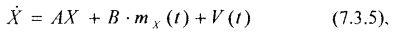
которое может быть решено при начальном условии:

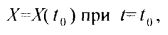
где:

- вектор X размерности (Nxl) по терминологии, принятой в теории управления динамическими системами, описывает «состояние» динамической системы и в этом смысле может быть назван вектором состояния финансового рынка;

- матрица коэффициентов А дифференциального уравнения (7.3.5) имеет размерность (NxN);

- матрица коэффициентов В имеет размерность (NxN), и её структура и значения коэффициентов выбираются таким образом, чтобы обеспечить условие астатизма воспроизведения векторной функции m_x(t);

m_x(t) – векторная функция, соответствующая математическому ожиданию векторного случайного процесса X(t);

V(t) – векторный случайный процесс белого шума (т. е. некоррелированный случайный процесс, имеющий корреляционную функцию в виде дельта-функции Дирака) с математическим ожиданием, равным нулю.

Известно, что векторное дифференциальное уравнения типа (7.3.5) эквивалентно системе скалярных дифференциальных уравнений. Применительно к обращению на рынке М финансовых инструментов соответствующее векторное дифференциальное уравнение можно представить в виде системы дифференциальных уравнений:

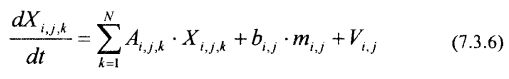
при начальных условиях:

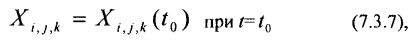
где:

i = 1,…,M – порядковый номер финансового инструмента, обращающегося на финансовом рынке;

j = 1,…, L – порядковый номер производной соответствующего случайного процесса;

N = M + L;

X_{i, j, k} – случайный процесс, например, случайное значение текущей доходности i-го финансового инструмента или же значение его j-й производной.

Из выражения (7.3.6) видно, что каждый i-й финансовый инструмент описывается системой, состоящей из j дифференциальных уравнений 1-го порядка. Это объясняется тем, что фактически каждому i-му финансовому инструменту соответствует дифференциальное уравнение формирующего фильтра порядка L. Вместе с тем в канонической форме Коши дифференциальное уравнение порядка L может быть представлено как система, состоящая из L дифференциальных уравнений первого порядка. С учетом того, что общее число обращающихся на рынке финансовых инструментов мы приняли равным М, общая размерность N системы (7.3.6) равна N = M + L.

Дифференциальное уравнение вида (7.3.5) и соответствующая ему система (7.3.6), с учетом того факта, что в правой части указанных уравнений присутствует случайный процесс белого шума, называются стохастическими дифференциальными уравнениями.

Известно, что решение матричного дифференциального уравнения (7.3.5) с правой частью будет иметь вид:

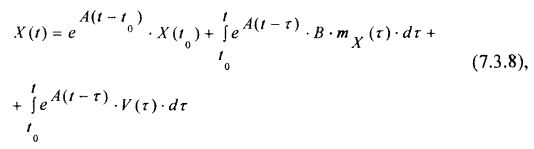
где e^{A(t – t₀)} – фундаментальная матрица решений дифференциального уравнения (7.3.5) в виде матричной экспоненты.

Переходя к математическим ожиданиям и учитывая, что математическое ожидание белого шума равно нулю, формула для вычисления математического ожидания векторного случайного процесса X(t), являющегося решением дифференциального уравнения (7.3.5), будет иметь вид:

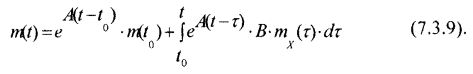
Применительно к математическому ожиданию этот результат почти очевиден, т. к. по условию в правой части дифференциального уравнения (7.3.5) фигурирует математическое ожидание процесса X(t). Однако существенно большие трудности возникают при вычислении ковариационной функции случайного процесс X(t) через выражение (7.3.8), определяющее решение дифференциального уравнения (7.3.5). Все сложности начинаются с того, что в этом случае необходимо знать фундаментальное решение дифференциального уравнения (7.3.5) без правой части, т. е. необходимо знать фундаментальное решение однородного дифференциального уравнения вида:

при начальных условиях:

В общем случае найти фундаментальное решение уравнения (7.3.10) достаточно трудно. Поэтому, в рамках корреляционной теории для нахождения моментов первого и второго порядка (указанный подход можно распространить для моментов любого порядка) используют подход, связанный с решением дифференциальных уравнений для моментов.

Учитывая всё сказанное выше о модели финансового рынка как стохастической дифференциальной системы, на него полностью распространяются все результаты теории стохастических дифференциальных систем. Поэтому ниже приводится сводка окончательных результатов в виде дифференциальных уравнений для моментов векторного случайного процесса:

Дифференциальное уравнение для математического ожидания вектора состояния финансового рынка:

при начальном условии:

По условиям формирования модели рынка (7.3.5) и при условии равенства матриц А=В, получим установившееся решение уравнения (7.3.12) в виде:

Дифференциальное уравнение для ковариационной матрицы:

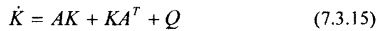
начальное условие:

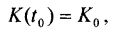
где:

Q – ковариационная матрица возбуждающего процесса типа белого шума в правой части дифференциального уравнения (7.3.5);

А – матрица коэффициентов дифференциального уравнения (7.3.5);

K(t) – ковариационная матрица имеет структуру:

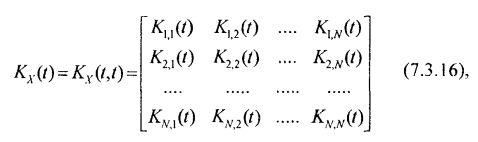
где:

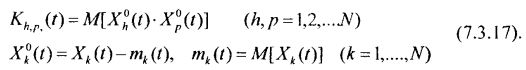
Дифференциальное уравнение для начального момента второго порядка:

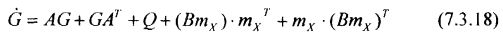
Матрица G(t) имеет структуру:

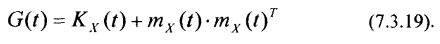
Интегрируя дифференциальное уравнение (7.3.18) после дифференциального уравнения (7.3.12), определяющего вектор математического ожидания векторного случайного процесса X(t), при начальном условии:

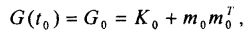
можно вычислить начальный момент второго порядка вектора состояния финансового рынка X(t).

Дифференциальное уравнение в частных производных для матрицы ковариационных функций (ковариационная функция векторного случайного процесса):

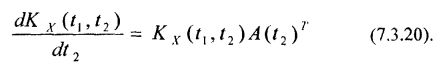
Начальное условие для уравнения (7.3.20) имеет вид K_X(t₁, t₂) = К_X(t₁), при этом матрица корреляционных функций имеет структуру:

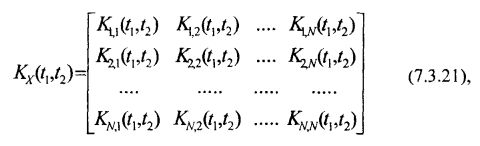
где:

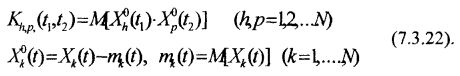
Ниже на рис. 7.4 представлена математическая модель финансового рынка в непрерывном времени в виде формирующего фильтра случайного процесса X(t) в соответствии с дифференциальным уравнением (7.3.5).

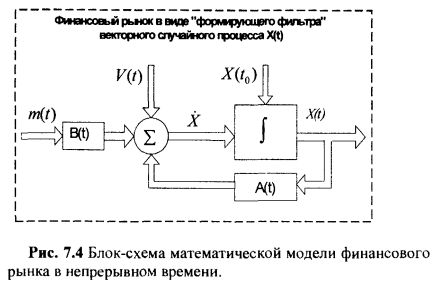
Математическая модель финансового рынка в дискретном времени

Рассмотрим далее модели финансового рынка в дискретном времени. Для этого рассмотрим векторно-матричное дифференциальное уравнение (7.3.5).

Связь между значениями вектора состояния финансового рынка для двух следующих друг за другом моментов времени вытекает из формулы для общего решения дифференциального уравнения (7.3.5). В указанной формуле через Ф обозначена переходная матрица для матрицы А в уравнении (7.3.5). Для двух следующих друг за другом моментов времени будем иметь:

Управляющее воздействие будем считать кусочно-постоянным, т.е.:

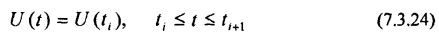
В целях упрощения обозначений примем следующее. Моменты времени t_i будут нумероваться целыми числами “i”. Таким образом,

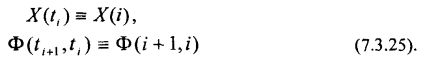
Положим далее:

Из свойств переходной матрицы следует, что A(i) всегда не вырождена.

При кусочно-постоянном управляющем воздействии можно вынести U(t_i) = U(i) из-под знака интеграла в выражении (7.3.23) и положить:

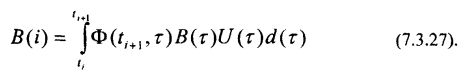
Дискретный аналог возбуждающего случайного процесса в правой части дифференциального уравнения (7.3.5) может быть получен, если положить:

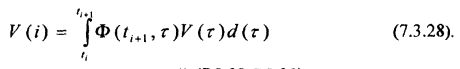
Из полученных соотношений (7.3.23-7.3.28) вытекает дискретный вариант непрерывной модели финансового рынка в виде:

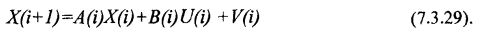
Выражение (7.3.29) является разностным уравнением формирующего фильтра и является дискретным аналогом дифференциального уравнения (7.3.5). Это уравнение описывает процесс функционирования финансового рынка в дискретном времени.

Содержание

Далее