7.3.3. Синтез конкретных моделей финансового рынка
При построении математической модели финансового рынка будем полагать что:
- процесс функционирования финансового рынка целиком определяется через обращающиеся на рынке базовые активы (ценные бумаги и основные мировые валюты);
- осуществляется регулярная котировка курсов всех инструментов финансового рынка и обеспечена 100% ликвидность соответствующих финансовых инструментов;
- изменения курсов (котировок) базовых финансовых инструментов при их рассмотрении в функции времени являются реализациями случайных процессов (случайных последовательностей).
Если рассматривать множество обращающихся на финансовом рынке инструментов, каждый из которых представлен собственным случайным процессом, то результирующий процесс, характеризующий рынок в целом, будет векторным. В указанной ситуации координатами этого векторного процесса будут являться локальные случайные процессы котировок отдельных финансовых инструментов.
Подобный подход открывает путь построения статистической модели финансового рынка и последующего использования математических методов теории оптимального управления для синтеза оптимальных стратегий инвестирования и биржевых спекуляций.
Отметим, что при построении соответствующих моделей в рамках рассматриваемой нами статистической концепции функционирования рынка, мы не будем делать различий между спотовым и срочным рынком. Это связано с тем, что для нас важен лишь сам факт регулярных котировок финансовых инструментов и совершенно безразличны любые другие их атрибуты.
Для простоты изложения мы ограничимся рассмотрением лишь линейной модели финансового рынка и обращающихся на нём инструментов в виде систем линейных дифференциальных и разностных уравнений. Синтез математической модели будем осуществлять в рамках корреляционной теории случайных процессов.
Путь построения конкретных математических моделей финансового рынка может состоять в следующем:
1. Предварительно должны проводиться статистические исследования рынка, результатом проведения которых должно являться:
1.1 Получение оценок автоковариационных функций отдельных финансовых инструментов.
1.2 Оценки смешанных моментов (взаимно-ковариационных функций) для различных финансовых инструментов.
1.3 Оценки для функций математических ожиданий рассмат риваемых случайных процессов.
2. На основе полученных оценок моментных характеристик случайных процессов необходимо идентифицировать параметры соответствующих дифференциальных (для дискретного времени – разностных) уравнений формирующих фильтров, которые в статистическом смысле будут описывать изменение вектора состояния финансового рынка.
При построении соответствующих моделей финансового рынка и обращающихся на нём финансовых инструментов наиболее удобно в качестве случайных координат вектора состояния рынка рассматривать ЭФФЕКТИВНОСТИ обращающихся на нём инструментов, а также возможно их производные до 2-го порядка включительно. Понятие эффективности (доходности) финансовых инструментов мы ранее подробно рассматривали в разделе 6 книги. Здесь мы ограничимся напоминанием основных моментов.


Понятия эффективности (доходности) финансовых инструментов является базовым, и оно должно вводиться для любых инструментов, обращающихся на том или ином рынке. Формула для оценки эффективности, как отмечалось ранее, имеет вид:

По экономическому смыслу эффективность финансового инструмента (7.3.30) определяет относительную скорость роста каждого рубля (или другой единицы валюты), вложенного в соответствующий финансовый инструмент. Существуют также другие модификации формулы (7.3.30), когда эффективность может быть выражена в процентах или же процентах годовых. Очевидно, что численные значения эффективности, определяемые формулой (7.3.30), а также производные эффективности вплоть до 2-го порядка включительно также являются случайными процессами (случайными последовательностями).
Ниже кратко рассматриваются примеры построения стохастических моделей отдельных финансовых инструментов и рынка в целом.
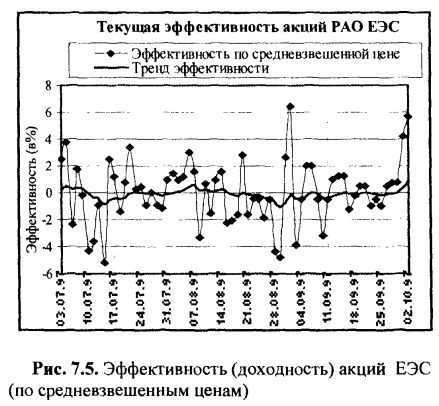
Пример 1. Требуется построить математическую модель для акций РАО ЕЭС России в виде разностного уравнения 1-го порядка, описывающего случайный процесс изменения эффективности указанной акции (по средневзвешенным ценам). При построении модели использовать результаты статистических исследований, представленных на рис. 7.5.
Решение. На рис. 7.5 приведены реализации случайного процесса эффективности (по средневзвешенным ценам) для акций РАО ЕЭС и, соответственно, тренд эффективности (функция математического ожидания эффективности).
На рис. 7.6 представлены оценки выборочной автоковариационной функции эффективности (по результатам статистической обработки первичного процесса эффективности – см. рис. 7.5), а также её аппроксимация с помощью автоковариационной функция динамического звена первого порядка. В качестве критерия «близости» аппроксимации принято совпадение значений соответствующих автоковариационных функций при единичном сдвиге.
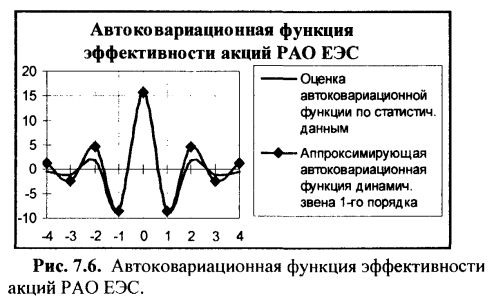
Из рисунка 7.6 легко видеть, что выражение для аппроксимирующей автоковариационной функции (динамического звена 1-го порядка) может быть представлено в виде:
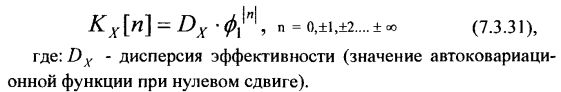
С учетом известных результатов теории указанному выражению (7.3.31) для автоковариационной функции соответствует разностное уравнение 1-го порядка:

разностного уравнения (7.3.32) будет случайный процесс с автоковариационной функцией вида (7.3.31).
В общем случае математическое ожидание эффективности (тренд эффективности) может являться ненулевой функцией времени. Тогда для оценивания тренда можно использовать различные низкочастотные математические фильтры, например, различные операторы авторегрессии-скользящего среднего, фильтры Калмана, наблюдатели Луэнбергера, Хаддля и т. п. Указанные математические фильтры при специальном подборе их параметров могут обеспечить получение несмещенных текущих оценок математического ожидания (в функции времени) с минимальной средиеквадратической ошибкой. Попутно отметим, что самую высокую точность оценивания обеспечивают фильтры Калмана.
С учетом сказанного, разностное уравнение (7.3.32) можно уточнить для случая ненулевого математического ожидания в виде:
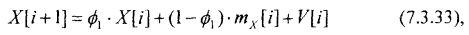
где: тx[i] – текущая оценка математического ожидания, получаемая с помощью тех или иных низкочастотных математических фильтров, параметры которых должны быть настроены исходя из условия обеспечения минимума среднеквадратической ошибки оценивания.
Разностное уравнение (7.3.33) будет определять случайный процесс с ненулевым математическим ожиданием, при этом центрированный (относительно математического ожидания) случайный процесс будет иметь автоковариационную функцию вида (7.3.31). На этом рассмотрение примера можно закончить.
Прежде, чем рассматривать конкретные модели для финансового рынка, уточним ранее полученные в разделе 7.2.2 математические модели.
Как отмечалось нами ранее в разделе 7.2.2, в рамках корреляционной теории случайных процессов математической моделью финансового рынка может служить векторно-матричное дифференциальное уравнение формирующего фильтра в виде:
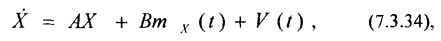
при начальных условиях:

где:
- вектор-столбец «X» размерности “Nx1” по терминологии, принятой в теории управления динамическими системами, описывает «состояние» динамической системы;
- матрицы «А» и «В» коэффициентов дифференциального уравнения (7.3.34) соответствующих размерностей;
- mx(t) – векторная функция, соответствующая математическому ожиданию векторного случайного процесса X(t);
-V(t) – векторный гауссовский случайный процесс «белого» шума (т. е. случайный процесс, имеющий корреляционную функцию в виде дельта-функции Дирака) с математическим ожиданием, равным нулю.
Векторно-матричное разностное уравнение, описывающее процесс функционирования финансового рынка в дискретном времени с учётом результатов раздела 7.2.2 может быть представлено в виде:

Разностное уравнение для ковариационной матрицы векторной случайной последовательности, описываемой уравнением (7.3.36), будет иметь вид:
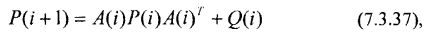
где P(i) – ковариационная матрица случайного процесса X[i] имеет размерность (NxN), при этом остальные обозначения в уравнении (7.3.37) аналогичны обозначениям для уравнения (7.3.36).
Структурная схема математической модели финансового рынка в дискретном времени, с учётом разностного уравнения (7.3.36), представлена ниже на рис. 7.7 в виде блок-схемы:
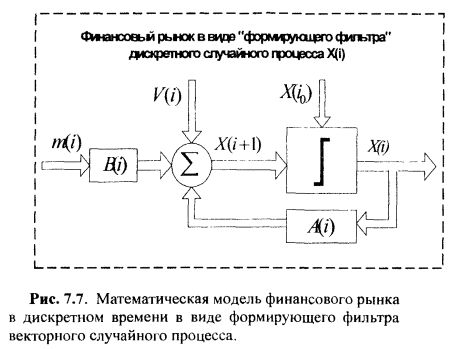
Приведённых выше сведений вполне достаточно для синтеза конкретной стохастической модели финансового рынка. Покажем это на следующем примере.
Пример 2. По результатам предварительных статистических исследований оценены элементы ковариационной матрицы P(i, i) и той же ковариационной матрицы P(i+1, i) при единичном сдвиге.
Требуется синтезировать дифференциальную стохастическую модель рынка в виде векторно-матричного разностного уравнения (формирующего фильтра).
Некоторые замечания.
1. Для упрощения рассматриваемого примера будем полагать, что вектор m(i)=0 (в 7.3.36), при этом процесс X(i) является стационарным. Это означает, что матрицы A(i)=A=Const, и Q(i)=Q=Const(cM.13.36, 7.3.37).
2. На главной диагонали ковариационной матрицы P(i) расположены дисперсии компонент векторного случайного процесса X(i), а другими элементами ковариационной матрицы являются смешанные моменты, определяющие ковариации между различными финансовыми инструментами, обращающимися на рынке.
Понятие «единичного сдвига» при оценивании элементов ковариационной матрицы эквивалентно единичному сдвигу при оценивании автоковариационной функции (см. «пример 1», рис. 7.3.2), только указанное понятие распространяется для всех элементов ковариационной матрицы.
Решение. Из уравнения (7.3.36) видно, что соответствующая стохастическая модель рынка определяется параметрами соответствующего разностного уравнения, а именно структурой и параметрами переходной матрицы A(i) и интенсивностью возбуждающего случайного процесса V(i) (т. е. структурой и параметрами матрицы Q(i) в уравнении 7.3.37). Поэтому процесс синтеза математической модели рынка сводится к синтезу структуры и параметров соответствующих матриц. Известно, что матрица A(i)=A в уравнении (7.3.36) формирующего фильтра марковского векторного случайного процесса может быть вычислена из выражения:
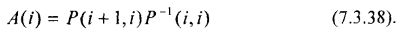
Подставляя в выражение (7.3.38) ковариационные матрицы P(i+1, i) и P(i, i), оцененные по результатам предварительных статистических исследований, однозначно определим структуру и параметры переходной матрицы A(i)=A=Const в модели (7.3.36). Структуру и параметры матрицы Q(i)=Q=Const определим из решения разностного уравнения (7.3.37). Указанное уравнение в установившемся состоянии (когда матрица P(i+1)=P(i)) сводится к алгебраическому матричному уравнению в виде:

где матрица «А» может быть получена из выражения (7.3.38), а ковариационная матрица P=P(i,i) является результатом предварительных исследований (задается исходными данными). Из выражения (7.3.39) легко определить единственную неизвестную матрицу Q, на чём решение задачи синтеза дискретной математической модели финансового рынка можно считать завершённым.
|