7.4.4.1. Оптимальное оценивание и прогнозирование вектора состояния финансового рынка
Хорошо известно, что оптимальным по критерию минимума среднеквадратической ошибки оценивания состояния («текущего», «прошлого» и «будущего») динамической системы является алгоритм, называемый фильтром Р. Калмана. Все любые другие алгоритмы оценивания по точности могут лишь приближаться к точности оценивания, которую обеспечивает фильтр Калмана. Потенциально возможная точность оценивания, достигаемая указанным фильтром, обеспечивается благодаря тому, что структура и параметры указанного алгоритма предварительно настраиваются на «статистический портрет» оцениваемой динамической системы. Именно поэтому необходимо проводить предварительные статистические исследования финансового рынка, чтобы получить адекватную рынку математическую модель в виде системы дифференциальных (разностных) уравнений, и уже затем настроить соответствующий фильтр Калмана на полученную математическую модель финансового рынка.
С учетом уравнения динамической системы (финансового рынка) вида (7.4.2) уравнения канала измерений (вычислений) вида (7.4.3), а также известных результатов теории, соответствующие уравнения фильтра Калмана для несмещенного оценивания текущего состояния финансового рынка с минимальной средне-квадратической ошибкой, могут быть записаны в виде:

где – m(i) – оценка вектора математического ожидания случайного процесса эффективности рынка, при этом матрица ковариации ошибок оценивания и матрица усиления фильтра K(i) определяются из рекуррентных уравнений:
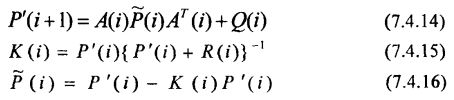
Начальные условия определяются выражением:

Здесь P(i0) – матрица ковариации начального вектора X(i0).
Она выражает соответствующую априорную информацию по оцениваемой динамической системе.


Оптимальный по критерию минимума среднеквадратической ошибки предсказания линейный многошаговый экстраполятор («предиктор») определяется на основе решения разностного уравнения (7.4.2), определяющего статистическую динамику финансового рынка. Переходя в указанном уравнении к математическим ожиданиям и рассматривая вместо мгновенного значения оцениваемого процесса его оптимальные оценки а, также используя формулу для решения разностного уравнения с правой частью, получим:

Покажем далее, как можно получить соответствующие оценки, не входя в противоречие с принципом каузальности (причинности) событий. Для этого рассмотрим одношаговый «предиктор», реализуемый фильтром Калмана:

где матрица усиления фильтра K'(i) определяется из уравнения (7.4.15), а ковариационная матрица для ошибки экстраполяции может быть получена из решения разностного уравнения вида:
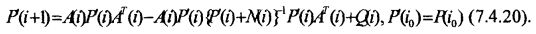
Уравнение (7.4.20) является дискретным аналогом известного матричного нелинейного дифференциального уравнения типа Риккати в задаче фильтрации с непрерывным временем. Последовательно применяя одношаговый «предиктор» (7.4.19), легко доопределить недостающие оценки m(τ), τ = i + 1, K – 1 в формуле (7.4.18) многошаговой экстраполяции («оптимального» предсказания).
Таким образом, выше были полностью определены алгоритмы оптимального оценивания и прогнозирования вектора состояния (эффективности) финансового рынка.
В результате применения указанных алгоритмов может быть синтезирована последовательность векторов предсказаний состояния рынка:

Эта последовательность векторов является исходной информацией для синтеза алгоритма динамической оптимизации принимаемых инвестиционных решений.
|