Оценка совместных вероятностей
Изложенный метод поквадрантной оценки совместных распределений вероятности при известных безусловных плотностях и коэффициенте корреляции между ними весьма привлекателен. Он точно описывает механизм формирования совместного распределения из компонентных безусловных распределений. Когда мы используем распределение Бернулли (распределение, у которого только два возможных исхода, т. е. сценарные спектры состоят только из двух сценариев), можно получить очень хорошую и простую оценку совместных вероятностей. Но чтобы сделать ее еще точнее, т. е. найти более детальные совместные вероятности, не ограничиваясь на квадрантах, требуется наперед знать коэффициенты корреляции составляющих квадрантов (или наперед знать совместные вероятности, чтобы, обратив формулу, получить коэффициенты корреляции).
При наличии зависимости совместные распределения будут изменяться под влиянием непосредственно предшествующих исходов.
Нередко нам будут известны не все коэффициенты корреляции между двумя сценарными спектрами, и поэтому мы будем вынуждены получить недостающие данные либо эмпирическим путем, либо с помощью оценки.
Если у вас имеются необходимые эмпирические данные, то рассчитать совместные вероятности совсем не сложно. Предположим, например, что вас интересуют совместные вероятности для двух акций – корпораций XYZ и ABC. У вас есть масса различных сценариев ожидаемого поведения цены каждой из них на следующий период владения (а период владения может быть любой единой длины по нашему выбору – это может быть день, два дня, неделя, месяц, год – что угодно). Один из сценариев спектра ABC соответствует подъему цены ее акций на два пункта. У вас также есть сценарий из спектра XYZ, соответствующий падению цены ее акций на полпункта. (Вместо абсолютных величин можно использовать изменения цены в процентах.) С помощью компьютера можно просчитать ценовые данные по обеим этим акциям и подсчитать, в скольких периодах владения акции ABC поднимались на два пункта, а акции XYZ – опускались на полпункта, и поделить полученную величину на общее количество периодов владения анализируемого массива данных. Затем мы можем проделать то же самое для каждой комбинации двух сценариев из наших сценарных спектров. То есть мы бы получили таблицу совместных вероятностей двух сценарных спектров эмпирическим путем.
Разумеется, располагая эмпирическими данными, можно сначала рассчитать требуемые коэффициенты корреляции, а затем на их основе построить таблицу совместных вероятностей.


Мы можем также оценить величины входящих в таблицу совместных вероятностей двух сценарных спектров. Делая это, нужно помнить о верхних и нижних границах каждой совместной вероятности, чтобы наши оценки не вышли за их пределы. Нижняя граница совместной вероятности, как вы помните, равна 0. Верхняя граница равна минимуму из двух индивидуальных вероятностей.
Кроме того, нужно, чтобы сумма всех совместных вероятностей в таблице строго равнялась 1,0.
Вспомните также, что каждая строка и каждый столбец таблицы совместных вероятностей двух сценарных спектров должны в сумме давать безусловную вероятность этой строки или столбца. Например, рассмотрим два различных сценарных спектра:
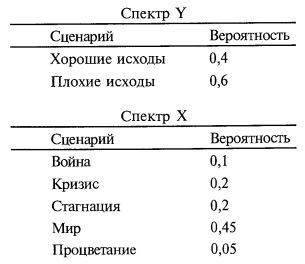
Исходя из этого, строим таблицу:

Из этого примера видно, что сумма вероятностей в первом столбце должна равняться безусловной плотности, ассоциированной со столбцом «Хорошие исходы» (0,4). То есть сумма совместных вероятностей «Войны», «Кризиса», «Стагнации», «Мира» и «Процветания», с одной стороны, и «Хороших исходов», с другой – должна быть строго равна 0,4.
Аналогично, сумма вероятностей в первой строке, то есть совместная вероятность «Хороших исходов» и «Войны» плюс совместная вероятность «Плохих исходов» и «Войны», должна равняться величине, ассоциированной с этой строкой, то есть с «Войной» (0, 1). Если взять последнюю строку «Процветание», то суммарно «Хорошие исходы» с «Процветанием» и «Плохие исходы» с «Процветанием» должны давать 0,5.
Заметьте, что если потребовать, чтобы совместные вероятности в каждой строке и в каждом столбце суммарно равнялись безусловной плотности, ассоциированной с каждой строкой и каждым столбцом (как и должно быть), то уже не нужно будет беспокоиться о том, чтобы ни одна совместная вероятность не превысила бы верхней границы (и, пока все ваши совместные вероятности больше или равны 0, как это и положено, не нужно беспокоиться о пересечении ими нижней границы). Кроме того, если совместные вероятности в каждой строке и в каждом столбце равны безусловным плотностям, ассоциированным с каждой строкой и каждым столбцом, то сумма всех совместных вероятностей в таблице будет строго равна 1,0 (в предположении, что сумма вероятностей в каждом сценарном спектре строго равна 1,0).
При возможности вам хорошо бы почаще сочетать оба метода определения совместных вероятностей. Конечно, если вам удастся раздобыть необходимые коэффициенты корреляции, то вы сможете получить совместные вероятности по формуле.
Наконец, когда вы группируете эмпирические данные, в качестве исходов групп используйте их медианы. Например, если в данных по доходам выделена группа 0–100 долл., в которую попадают три значения 10, 20 и 90 долл., то в качестве исхода этого сценария используйте медиану 20 долл.
Новая модель, представленная в следующей главе этой книги, отличается математической строгостью. Единственными исходными данными, которых она требует, являются сценарии, то есть вероятности всевозможных исходов. Они играют первостепенную роль при оценке совместных (условных) вероятностей. Если вероятности неточны, то и отдача от новой модели будет невелика. Проблема заключается в том, чтобы точно назначать совместные вероятности возможным исходам многих одновременных сценарных спектров. Достижение вершины (n + 1)-мерного изображения столь же важно, как и усилия по таймингу и выбору сделки. Эту вершину (как и любую другую точку, в которой мы хотели бы находиться) дает нам новая модель столь же точно, сколь точно мы оценили совместные вероятности. Поэтому мы можем утверждать, что оценка совместных вероятностей, безусловно, так же важна, как и усилия по таймингу и выбору сделки. А, возможно, и более важна, ибо мы сами контролируем наши оценки, а решать, будет ли следующая сделка прибыльной или нет, мы не можем.
|