Целевая функция

Целевая функция, которую мы хотим максимизировать, представляет собой среднее геометрическое от HPR, которое обозначается просто G:

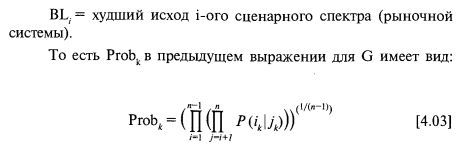
Величина P(i_k|j_k) – это просто совместная вероятность (предмет обсуждения предыдущей главы) сценариев i-го и j-го спектров, которые входят в k-ую комбинацию сценариев. Например, если у нас есть три монеты, то каждой из них соответствует сценарный спектр из двух сценариев: орел и решка. Количество сценарных спектров (2) выражается переменной n. Откуда получаем восемь (2 * 2 * 2) возможных комбинаций исходов, которые обозначаются переменной m.

В выражении [4.01] переменная к изменяется от 1 до m в одометрическом (лексикографическом) порядке:

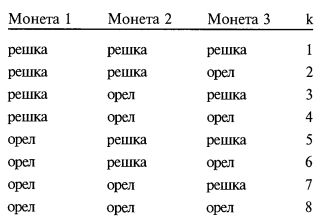
То есть изначально все спектры установлены на свои худшие (крайне левые) значения. Затем крайне правый спектр циклически проходит через все свои значения, после чего второй справа спектр переходит к следующему (справа) сценарию. Продолжаем таким образом дальше: циклически меняем все сценарии крайне правого спектра, когда второй справа сценарный спектр циклически прошел все свои значения, третий переходит к своему следующему сценарию. Данный процесс абсолютно аналогичен тому, как работает одометр в автомобиле, откуда и взялось название одометрический.

Таким образом, если бы к было больше 3 (т. е. k = 3), i равно 1, a j равно 3, то величина P(i_k|j_k) обозначала бы совместную вероятность выпадения монеты 1 решкой и выпадения монеты 3 решкой. Наконец, подставив выражения [4.02] и [4.03] в [4.01], мы можем создать одну полную целевую функцию. То есть мы сможем максимизировать G в виде:

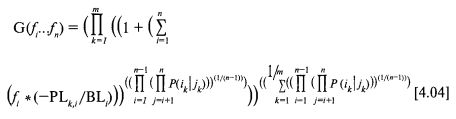
Данная целевая функция, которую нам нужно максимизировать, выражает суть нашей новой методологии инвестирования капитала. Она дает нам высоту, среднее геометрическое HPR, в (п + 1)-мерном пространстве используемых значений f. Это точное значение, безотносительно к тому, как много сценарных спектров используется в качестве аргументов. Это – целевая функция модели в пространстве рычагов.

Хотя выражение [4.04] может показаться несколько устрашающим, нет никаких причин пугаться его. Как можно заметить, это выражение представляет собой компактную форму выражения [4.01], с которой работать много удобнее.

Возвращаясь к нашему примеру с тремя монетами, предположим, что мы выигрываем два доллара на выпадении орла и проигрываем один доллар на выпадении решки. У нас имеется три сценарных спектра, три рыночных системы, называемые Монета 1, Монета 2 и Монета 3. Два сценария, орел и решка, представляют каждую монету, каждый сценарный спектр. Для простоты будем предполагать, что взаимные коэффициенты корреляции всех трех сценарных спектров (монет) равны 0.

Следовательно, мы должны найти три различных значения f. Мы отыскиваем оптимальное значение f для Монеты 1, Монеты 2 и Монеты 3, обозначаемые через f₁, f₂ и f₃ соответственно, которые дают наибольший рост, то есть комбинацию трех значений f, которые приводят к наибольшему среднему геометрическому HPR (выражение [4.01] или [4.04]).

В данный момент мы не обращаем никакого внимания на избранный метод оптимизации. Сейчас наша цель заключается в том, чтобы показать, как вычисляется целевая функция. Поскольку методы оптимизации обычно назначают переменным некоторые начальные значения, мы произвольно выбираем 0,1 в качестве начального значения для всех трех величин f.

Для простоты вместо формулы [4.04] мы будем использовать выражение [4.01]. Исходя из него, мы начнем перебирать все комбинации сценарных наборов по возрастанию индекса к от 1 до т, вычисляя HPR комбинаций сценарных наборов по формуле [4.02] и перемножая все эти HPR вместе. Каждый раз, вычисляя выражение [4.02], нужно отслеживать показатели степени в фигурных скобках, ибо далее нам понадобится их сумма.

Итак, мы начинаем с k = 1, где сценарный спектр 1 (Монета 1) поворачивается решкой, как и два других сценарных спектра (монеты).

Формулу [4.02] можно переписать в виде:

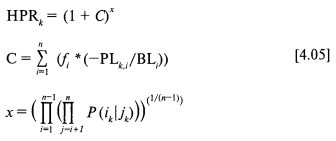
Заметьте, что помещенный в скобки показатель степени в формуле [4.02], который мы должны отслеживать, в формуле [4.05] обозначен переменной х. Его же представляет и [4.03].

Таким образом, для получения С мы действуем следующим образом. Проходя через каждый сценарный спектр, берем исход текущего сценария согласно значению индекса к и делим его отрицательное значение на величину наихудшего исхода в данном спектре. Полученное частное умножаем на значение f, которое используется с данным сценарным спектром. По мере продвижения от одного сценарного спектра к другому эти величины суммируются.

Индекс i обозначает тот сценарный спектр, который мы рассматриваем в текущий момент. Наибольшая потеря в сценарном спектре 1, происходящая при выпадении решки, составляет один доллар (т.е. –1). Следовательно, BL₁ равен –1 (каковыми будут и BL₂, и BL₃, поскольку наибольшая потеря в каждом из двух других сценарных спектров, или на двух других монетах, равна –1). Ассоциированная величина PL, то есть исход того сценария в i-ом спектре, который соответствует тому сценарию этого спектра, на который указывает k, равна –1 в сценарном спектре 1 (так же, как и в двух других спектрах). В данный момент значение f равно 0,1 (как это сейчас и в двух других спектрах). Итак:

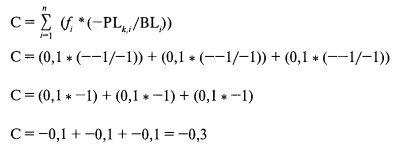
Обратите внимание, что значения PL отрицательны, поэтому выражения во внутренних скобках положительны.

Теперь берем значение для С из формулы [4.05], прибавляем к нему 1 и получаем 0,7 (так как 1 + (-0,3) = 0,7). Теперь мы должны определить показатель степени, или переменную х из формулы [4.05].

Величина P(i_k|j_k) обозначает просто совместную вероятность k-го сценария из i-го спектра и k-го сценария из j-го спектра. Поскольку индекс к в данный момент равен 1, то он указывает на выпадение решки во всех трех сценарных спектрах. Значение х находим следующим образом. Берем произведение совместных вероятностей сценариев из спектров 1 и 2, умножаем его на совместную вероятность сценариев из спектров 1 и 3 и на совместную вероятность сценариев 2 и 3. Иначе это можно выразить так:

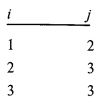
Если бы имелось четыре спектра, то мы бы взяли произведение всех совместных вероятностей согласно схеме:

Поскольку все наши совместные вероятности равны 0,25, для х получаем:

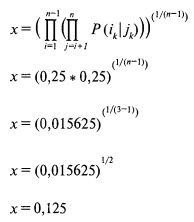
Таким образом, х, равное 0,125, составляет совместную вероятность k-й комбинации сценариев. (Отметьте, что мы собираемся определить совместную вероятность трех случайных переменных с использованием совместных вероятностей двух случайных переменных!)

Отсюда HPR_k = 0,7^0,125 = 0,9563949076, когда k = 1. С помощью формул [4.02] или [4.05] мы должны вычислить эту величину для всех значений к от 1 до m (в данном случае m равно 8). Проделав это, получим:

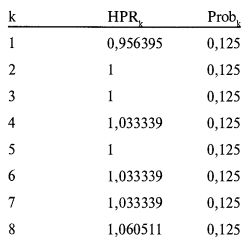
Суммирование по формуле [4.04] всех Prob_k, получаемых из [4.03], дает 1. Далее, перемножив все HPR, согласно [4.01] или [4.04], получим 1,119131. Откуда следует, что величина G из [4.01], равная 1,119131, отвечает значениям 0,1, 0,1, 0,1 величин f₁, f₂ и f₃ соответственно.

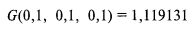
Далее, руководствуясь используемым методом математической оптимизации, мы стали бы изменять наши значения f. В итоге мы нашли бы оптимальные значения 0,21, 0,21, 0,21 для f₁, f₂ и f₃, соответственно. Это дало бы нам:

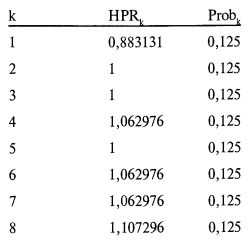
Эти данные получаются по формуле [4.01] следующим образом:

Данная комбинация значений f дает наибольшее G для заданных сценарных спектров. Поскольку это очень упрощенный случай, то есть все сценарные спектры одинаковы и корреляция между ними нулевая, мы получили одинаковые значения (0,21) для всех сценарных спектров. Обычно так не бывает, и вы получите свое значение f для каждого сценарного спектра.

Теперь, когда мы знаем оптимальные значения для всех сценарных спектров, мы можем определить, насколько велики эти десятичные величины в денежном выражении. Для этого разделим наихудший исход (потерю) сценариев каждого спектра на отрицательное значение оптимального f этого спектра. Например, для первого сценарного спектра, Монеты 1, максимальная потеря была равна –1. Деля –1 на отрицательное оптимальное f, –0,21, получаем 4,761904762 в качестве значения f$ для Монеты 1.

Подведя итоги, укажем:

1. Начните с некоторого набора значений f для f₁... f_n, где п – количество компонент в портфеле, т. е. рыночных систем или сценарных спектров. Начальный набор значений f задается используемым методом оптимизации.

2. Переберите комбинации сценарных наборов в одометрическом порядке по индексу k от 1 до т, для каждого k вычислите HPR и перемножьте их вместе. Попутно ведите текущую сумму показателей степени, в которые возводятся эти HPR.

3. Вычислите последнее HPR при к = т. Возведите последнее произведение в степень, обратную сумме показателей (вероятностей) всех HPR, и получите G – среднее геометрическое HPR.

4. Это среднее геометрическое HPR дает нам высоту в (п + 1)-мерном пространстве. Нам нужно найти вершину в этом пространстве, поэтому далее нам следует выбрать и опробовать новый набор значений f, который помог бы нам найти эту вершину. Этот процесс и называется математической оптимизацией.

Содержание

Далее