Страхование портфеля и оптимальное f
Предположим на время, что вы управляете инвестиционным фондом. На рис. 5.2 демонстрируется типичная тактика страхования портфеля, известная также как динамичное хеджирование. В этом примере точкой отсчета является текущая стоимость портфеля 100 долл. за акцию. Обычный портфель будет точно следовать за рынком акций. Этот случай отображается непрерывной линией. Застрахованный портфель отражается прерывистой линией. Вы видите, что прерывистая линия расположена под непрерывной, когда портфель находится на своей начальной величине 100 или больше долларов. Разница между ними отображает стоимость проведения портфельного страхования. В ином случае, когда величина портфеля падает, страхование портфеля поддерживает его минимальную величину на желаемом уровне (в данном случае – это текущая стоимость 100 долларов за акцию) минус стоимость реализации данной тактики.
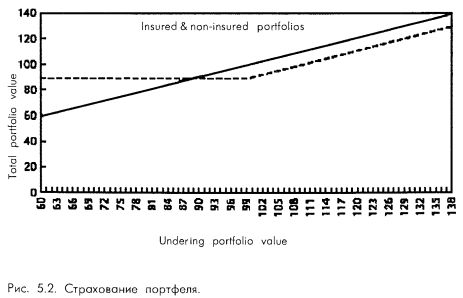
По сути, страхование портфеля сродни покупке пут-опциона на этот портфель. Предположим, что фонд, которым вы управляете, состоит лишь из одной акции, текущая стоимость которой равна 100 долл. Покупка пут-опциона на эту акцию с ценой исполнения 100 долл. и стоимостью 10 долл. скопировала бы прерывистую линию на рис. 5.2. Худшее, что может случиться с вашим портфелем из этой акции и пут-опциона на него, состоит в том, что вы исполните пут, в результате чего продадите акцию за 100 долл. и потеряете на этом стоимость пута – 10 долл. То есть самая меньшая стоимость портфеля составит 90 долл., независимо от того, как бы низко ни упала базовая акция.
При высоких ценах акции ваш застрахованный портфель теряет часть прибыли от того, что его стоимость всегда сокращается на цену пута.


Теперь примем во внимание, что покупка колл-опциона даст тот же результат, что и покупка базового актива вместе с покупкой пут-опциона с такими же ценой и датой исполнения, как у колл-опциона. Когда мы говорим об одинаковом результате, мы имеем в виду эквивалентность позиции в смысле показателей риск/прибыль при различной стоимости базового актива. Поэтому прерывистая линия на рис. 5.2 может также представлять портфель, который может быть составлен из длинной позиции по колл-опциону ценой в 100 долл. при его истечении.
Вот как действует динамичное хеджирование при обеспечении портфельного страхования. Предположим, что вы покупаете для своего фонда 100 долей этой единственной акции по цене 100 долл. за штуку. Теперь вы реплицируете (воспроизводите) колл-опцион с использованием данной базовой акции. Вы сделаете это путем задания начального минимума для акции. Пусть этот определенный вами минимум равен 100. Вы также зададите дату истечения этого гипотетического опциона, который вы собираетесь создать. Пусть назначенная вами дата истечения падает на конец текущего квартала.
Теперь вы определите дельту (текущую скорость изменения цены колл-опциона при изменении цены базового инструмента) для этого 100-долларового колл-опциона с выбранной датой истечения. Предположим, что эта дельта равна 0,5. Это значит, что вы должны инвестировать 50% вашего капитала в данную акцию. То есть у вас было бы только 50 этих акций вместо 100 штук, которые вы бы имели, не используй вы страхование портфеля. С ростом цены акции то же происходит и с дельтой, а равно и с количеством акций в вашем распоряжении. Верхним пределом дельты является 1, где вы были бы инвестированы на 100%. В нашем примере при дельте, равной 1, у вас было бы 100 акций.
При понижении акции то же происходит и с дельтой. Аналогичным образом сокращается и величина позиции по данной акции. Нижним пределом дельты является 0, где у вас не было бы позиции по данной акции.
На практике управляющие фондами применяют неагрессивные методы динамичного хеджирования. Они не предусматривают необходимости торговли портфелем из наличных акций. Вместо этого портфель, в целом, подстраивается к тому, какой должна быть текущая дельта, величина которой диктуется моделью использования фьючерсов на индексы акций и иногда пут-опционов. Одно из преимуществ метода использования фьючерсов состоит в том, что они имеют низкие операционные издержки.
Короткая продажа фьючерсов против портфеля эквивалентна продаже части портфеля и обращения ее в наличность. При снижении стоимости портфеля продается больше фьючерсов, а при росте его стоимости эти короткие позиции покрываются. Ущерб портфелю, когда он растет, а короткие фьючерсные позиции покрываются, составляет цена страхования портфеля, или цена реплицированных пут-опционов. Достоинством динамичного хеджирования является то, что оно позволяет нам довольно точно оценивать эту цену в самом начале. Менеджерам, которые опробывают эту тактику, она позволяет сохранять портфель в неприкосновенности, в то время как необходимые изменения в распределении средств осуществляются за счет сделок с фьючерсами. Данная неагрессивная методика использования фьючерсов позволяет отделить размещение капитала от активного управления портфелем.
Те, кто использует страхование портфеля, должны постоянно корректировать портфель в соответствии с дельтой. Это означает, что для определения дельты пут-опциона, который вы стараетесь симитировать, вам нужно ежедневно подставлять в ценовую модель опциона текущую стоимость портфеля, время, оставшееся до истечения, уровни процентных ставок и волатильность портфеля. Прибавление этой дельты (представляющей собой число между 0 и –1) к 1 даст вам дельту соответствующего кола. Она представляет собой степень хеджирования, или процент, который вам следует инвестировать в данный фонд.
Предположим, что ваша степень хеджирования в настоящий момент составляет 0,46. Пусть объем фонда, которым вы управляете, эквивалентен пятидесяти фьючерсным единицам на индекс S&P. Поскольку вы хотите инвестировать только на 46%, значит, 54% вы оставляете незахеджированными. Пятьдесят четыре процента от пятидесяти единиц составляют двадцать семь единиц. Следовательно, на теперешнем ценовом уровне при данных уровнях процентных ставок и волатильности в настоящий момент фонд должен наряду с длинной позицией в акциях включать и короткую позицию из двадцати семи фьючерсных единиц на индекс S&P.
Поскольку нужно все время отслеживать соответствие портфеля и дельты, требующей постоянного пересчета, эта тактика хеджирования называется динамичной.
Использование фьючерсов в рамках данной тактики осложняется тем, что рынок фьючерсов не следует точно за наличным рынком. Далее, портфель, против которого вы продаете фьючерсы, может не вполне точно отслеживать сам индекс, лежащий в основе фьючерса. Такой дисбаланс может внести свой вклад в неустойчивость страхования портфеля. Более того, когда имитируемый опцион очень близко подходит к сроку своего истечения и стоимость портфеля приближается к цене исполнения, гамма этого опциона астрономически вырастает. Гамма – это текущая скорость изменения дельты, или степени хеджирования. Другими словами, гамма – это дельта дельты. Когда дельта изменяется очень быстро (т. е. если имитируемый опцион имеет высокую гамму), проведение страхования портфеля все больше осложняется. Есть множество способов справиться с этой проблемой, некоторые из которых весьма изощренные. Один из простейших опирается на концепцию бессрочного опциона. Вы, например, всегда можете предположить, что опцион, который вы имитируете, истекает, скажем, через три месяца. Каждый день вы станете сдвигать дату истечения опциона на один день вперед. Повторю, что эта высокая гамма обычно только тогда становится проблемой, когда приближается дата истечения и при этом очень близки цена портфеля и цена исполнения опциона.
Имеется очень интересная взаимосвязь между оптимальным f и страхованием портфеля. Когда вы открываете позицию, вы можете утверждать, что инвестированы f процентов ваших средств. Например, рассмотрим азартную игру, в которой ваше оптимальное f равно 0,5, наибольший проигрыш равен –1, а ресурсы – 10 000 долл. В данном случае вы стали бы ставить по одному доллару на каждые два доллара вашего счета, ибо –1, или наибольший проигрыш, деленный на –0,5, или на отрицательное оптимальное f, дает 2. Деля 10 000 долл. на 2, получаем 5000 долл. Следовательно, вы поставили бы на следующий кон 5000 долл., которые составляют f процентов (50%) вашего капитала. Если бы вы умножили величину своего капитала на f (0,5), то в результате пришли бы к тем же 5000 долл. Поэтому вы поставили на кон f процентов своего капитала.
Аналогичным образом, если бы наш наибольший проигрыш был равен 250 долл., а все остальное не изменялось, то мы бы делали одну ставку на каждые 500 долл. своего счета, ибо – 250 долл./–5 = 500 долл. Деление 10 000 долл. на 500 долл. показывает, что мы сделали бы двадцать ставок. Поскольку самое большее, что мы можем потерять на одной ставке, равно 250 долл., то тогда мы рисковали бы f процентами (50%) своего счета, играя 5000 долл. (250 долл. * 20).
Поэтому мы можем утверждать, что f равно тому проценту нашего капитала, которым рискуем, или что f равно коэффициенту хеджирования. Вспомните, что, обсуждая портфели, мы рассматривали сумму значений f его компонент. Поскольку при использовании метода динамичного дробления f мы применяем его только к активной части нашего портфеля, мы можем утверждать, что коэффициент хеджирования портфеля Н равен:

Выражение [5.10а] дает нам степень хеджирования портфеля, который торгуется на основе тактики динамичного дробления f. Страхование портфеля действует и при статичном дроблении f, только частное active$/общий капитал равно 1, а значение для f (оптимальное f) умножается на ту величину, которую мы используем в качестве доли f. Таким образом, при использовании статичного дробления f степень хеджирования равна:

Мы можем утверждать, что, торгуя счетом на основе динамичного дробления f мы проводим страхование портфеля. В этом случае минимум известен заранее и равен начальному пассивному капиталу плюс цена проведения страхования. Чаще, однако, за минимум при тактике динамичного дробления f проще принять начальные пассивные средства счета.
Мы можем утверждать, что выражения [5.10а или b] дают величину дельты колл-опциона, как ее понимают в портфельном страховании. Более того, мы обнаруживаем, что эта дельта во многом изменяется так же, как колл-опцион с глубоко «без денег» (deep out-of-the-money) и с очень отдаленным сроком истечения. Таким образом, благодаря использованию постоянной пассивной долларовой суммы торговля счетом согласно тактике динамичного дробления f эквивалентна обладанию пут-опционом с глубоко «в деньгах» (deep in-the-money) и с очень отдаленным сроком истечения. Аналогичным образом, мы можем утверждать, что торговля согласно тактике динамичного дробления f представляет собой то же самое, что владение колл-опционом на портфель с глубоко «без денег», и который очень долго не истекает.
Однако страхование портфеля можно также использовать и как метод перераспределения средств для управления их эффективностью. Это управление возможно аналогично попытке управлять танкером с помощью весла гребной лодки, но оно является ценным методом перераспределения. Данный метод предполагает, что сначала задаются параметры для программы. Во-первых, вы должны определить величину минимума. Выбрав ее, вы должны принять решения относительно даты истечения, уровня волатильности и других исходных параметров конкретной опционной модели, которую вы намереваетесь использовать. Эти параметры будут давать вам дельту опциона в любой данный момент времени. Как только дельта известна, вы можете определить, каким должен быть ваш активный капитал. Поскольку дельта для счета, или переменная Н в формуле [5.10а], должна равняться дельте имитируемого колл-опциона:
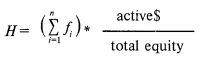
Поэтому:
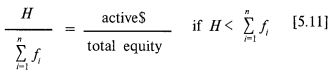
иначе:
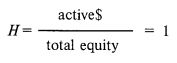
Поскольку дробь active$/общий капитал равна проценту активного капитала, мы можем утверждать, что доля средств, которую нам следует иметь в активной части капитала, равна дельте колл-опциона, деленной на сумму величин f компонентов портфеля. Однако вы заметите, что если Н больше суммы этих f, то это указывает на то, что вы определили в качестве активной части больше 100% капитала на вашем счете. Поскольку это невозможно, то существует верхний предел в 100% капитала на счете, который может быть использован в качестве активного.
Страхование портфеля прекрасно в теории, но слабо на практике. Как показал крах рынка акций 1987 г., беда портфельного страхования состоит в том, что когда цены падают в бездну, то ликвидности нет ни при какой цене. Однако здесь нас это не заботит, поскольку мы интересуемся соотношением между активным и пассивным капиталом и тем, насколько математически это похоже на страхование портфеля.
Проблема практического использования страхования портфеля в качестве метода перераспределения капитала, как было подробно показано выше, состоит в том, что перераспределение происходит постоянно. Это принижает тот факт, что тактика динамичного дробления асимптотически превзойдет тактику статичного дробления f. В результате попытки управлять эффективностью путем страхования портфеля как метода динамичного перераспределения f, вероятно, не является такой уж хорошей идеей. Однако всякий раз, когда вы используете дробление f, статичное или динамичное, вы пользуетесь некоей формой страхования портфеля.
|