Градиентная торговля и непрерывное доминирование
В этой книге, как и в двух предыдущих, мы продемонстрировали, что при заданной рыночной системе или сценарном спектре торговля на оптимальном f (или на наборе оптимальных f для нескольких одновременно действующих сценарных спектров или рыночных систем) даст асимптотически самый большой рост, то есть в итоге, по мере того, как количество периодов владения, в которые мы торговали, становится все больше и больше. Однако из Главы 2 мы узнали, что если у нас было конечное количество периодов владения и мы знаем, сколько периодов мы собираемся торговать, то действительно оптимальными будут такие величины, которые даже несколько агрессивнее, чем оптимальные f. То есть это те значения f которые максимизируют ожидаемый средний общий рост (EACG).
В конце концов, каждый из нас может проторговать только конечное число периодов владения – никто не будет жить вечно. Однако кроме редчайших случаев мы не знаем точной продолжительности этого конечного числа периодов владения. Поэтому в качестве следующего наилучшего приближения мы используем асимптотический предел.
Теперь же мы продемонстрируем метод, который можно использовать в данном случае неизвестного, но конечного числа периодов владения, в течение которых мы собираемся торговать на асимптотическом пределе (т.е. на оптимальных значениях f). Этот предел при торговле на разбавленном f (с помощью статичного или динамичного дробления) допускает доминирование не только асимптотическое, но и в течение любого заданного периода владения в будущем.


То есть теперь мы познакомимся с методом работы при разбавлении f (которое должно использоваться почти всеми управляющими капиталом для того, чтобы практические требования клиентов относительно падений величины торгового счета), который обеспечивает не только максимум капитала на счете в очень отдаленной перспективе, но и максимум счета в любой момент времени, каким бы близким или далеким он ни был! Более не нужно будет держаться за оптимальное f (или, в более широком смысле, держаться за нашу новую методологию), утешая себя мыслью о том, что в конечном итоге это принесет лучшие результаты. Наоборот, тот метод, который чуть ниже проиллюстрируем, нацелен на доминирование во все периоды времени!
Это является огромным продвижением вперед. Поскольку почти каждый будет разбавлять то, что служит их оптимальными значениями f, – либо осознанно, либо ненамеренно по незнанию – приемы, о которых идет речь, будут постоянно максимизировать прибыльность счета при разбавленных значениях f, а не только так, как это всегда было с максимизацией среднего геометрического, – в очень отдаленной перспективе.
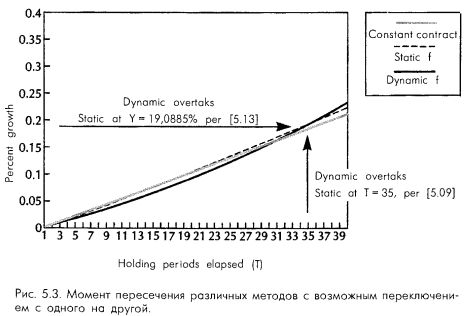
Вновь мы должны обратить наше внимание на функции и темпы роста. Посмотрите на рис. 5.3, на котором изображен рост (функция роста) в процентах от нашей начальной ставки. Теперь взгляните на рис 5.4, представляющий темп роста в процентах от нашей ставки.
На этих графиках вновь изображен начальный активный капитал в 20%, который используется для торговли как на динамичной, так и на статичной основе. Поскольку в обоих этих случаях торговля начинается с одного и того же количества единиц, то именно оно используется в качестве постоянного контракта при обычной торговле, которая также представлена на рис. 5.4. На этом графике использовалось среднее геометрическое HPR (на полном f), равное 1,01933, и, следовательно, среднее геометрическое при статичном дроблении f в 0,2 было равно 1,005, а среднее арифметическое HPR на полном f было – 1,0265.

Обратите внимание, что если постоянно использовать в торговле тот метод, который в данный момент имеет больший градиент, то с наибольшей вероятностью счет в любой момент времени будет в своей наибольшей части доступного капитала. Так, мы начинаем торговать на базе фиксированного контракта с числом единиц, равным тому, которым бы мы начинали торговлю при дробном f.
Далее, в тот момент (по времени или по приросту капитала), когда доминирует статичный градиент f, мы переключаемся на торговлю со статичным f. Наконец, когда доминирует динамичный градиент, мы переходим на торговлю на основе динамичного f. Обратите внимание, что, постоянно используя тот метод, у которого в данный момент наибольший градиент, вы всегда будете находиться на самой высокой кривой из трех, изображенных на рис. 5.3.
Функция роста Y для метода постоянного контракта теперь дается в виде:
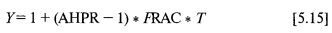
Функции роста берутся из формулы [5.09]. Таким образом, функция роста для статичного f является левой частью [5.09], а для динамичного f – правой. То есть функция роста для статичного f имеет вид:

И для динамичного f:
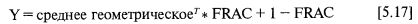
Формулы [5.15–17] дают нам функции роста в виде произведения нашей начальной ставки на заданное количество периодов владения Т. Поэтому, вычитая из [5.15-17] единицу, получаем процентный рост, который изображен на рис. 5.3.
Градиенты, изображенные на рис. 5.4., являются просто первыми производными по Т функций Y, заданных формулами [5.15–17]. То есть градиенты определяются следующим образом:
Для торговли постоянным контрактом:

Для статичного дробного f:

И наконец для динамичного дробного f:

где
T = количество периодов владения;
FRAC= начальный процент активного капитала;
среднее геометрическое = грубое среднее геометрическое при оптимальном f;
AHPR = арифметическое среднее HPR, задаваемое [5.07]; ln( ) = функция натурального логарифма.
Применяются эти формулы, особенно если ваши сценарии (сценарные спектры) и совместные вероятности изменяются от одного периода владения к другому, следующим образом. Вспомним, что перед каждым периодом владения мы должны определить оптимальные инвестирования. Для того чтобы сделать это, мы собираем всю необходимую информацию для получения значений переменных, перечисленных выше (FRAC, среднего геометрического, AHPR и аргументов функции [5.07] для определения FGHPR). Затем мы подставляем эти значения в формулы [5.18], [5.CAPut!'] и [5.20]. Та формула, которая дает больший результат, определяет наш метод торговли.
Чтобы проиллюстрировать это на примере, обратимся к знакомой нам игре в монетку «два-к-одному». Предположим, что это наш единственный набор сценариев, содержащий два сценария для орлов и решек. Предположим далее, что мы собираемся играть с долей 0,2 (т. е. одной пятой оптимального f). Таким образом, FRAC равно 0,2, среднее геометрическое равно 1,06066, и AHPR равно 1,125. Для определения FGHPR по формуле [5.07] у нас уже есть FRAC и AHPR, и нужно только SD – стандартное отклонение значений HPR, которое равно 0,375. Таким образом, FGHPR равно

Подстановка этих величин в три градиентные функции, задаваемые формулами [5.18–120], дает нам следующую таблицу:
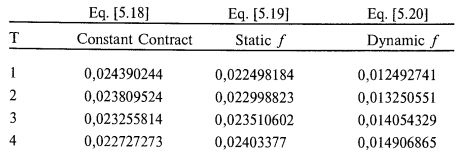
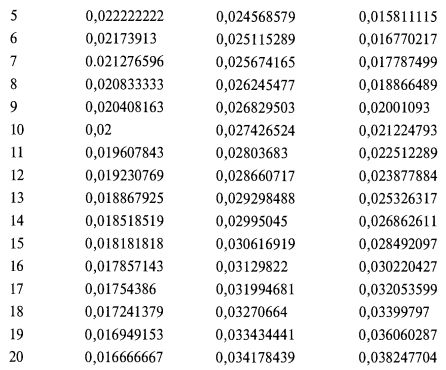
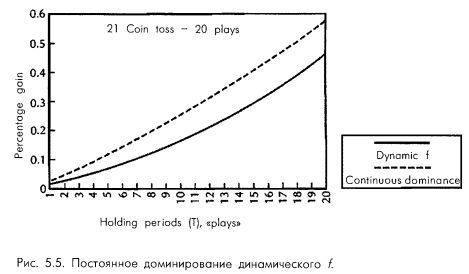
Мы видим, что наибольший градиент для двух первых периодов владения дает игра на основе постоянной ставки, а на третий период нам следует переключиться на статичное f. На семнадцатом периоде нам нужно переключиться на динамичное f. Если бы мы поступили таким образом, то, как это видно на рис. 5.5, за первые двадцать конов преуспели бы в среднем гораздо больше, чем при простом использовании метода динамичного f.
Обратите внимание, что в каждом периоде при описанном подходе ставка в игре имеет большее ожидаемое значение, чем даже при игре с динамичным дроблением f. Далее, начиная с семнадцатого периода, где мы переключились со статичного на динамичный метод, обе линии впредь имеют одинаковый градиент. То есть динамичная линия никогда не сможет «догнать» линию постоянного доминирования. Таким образом, принцип постоянной торговли с наибольшим градиентом для достижения постоянного доминирования помогает управляющему капиталом максимизировать величину счета в любой момент в будущем, а не только в асимптотическом смысле.
Продолжим пояснение на примере, предположив, что мы играем в монетку с начальным счетом в 200 долл. Наше оптимальное f равно 0,25, а 0,2f равно одной пятой этой величины, что означает, что мы играем со значением f, равным 0,5, или ставим один доллар на каждые двадцать долларов счета. Следовательно, на первый кон мы ставим десять долларов. Поскольку мы играем с постоянной ставкой, то независимо от состояния счета мы будем ставить столько же на каждый следующий кон, пока не перейдем на статичное f. Это происходит на третьем кону. Поэтому на третьем кону мы оцениваем наш счет и ставим один доллар на каждые двадцать долларов капитала. Пройдя таким образом до 16-го кона включительно, перед семнадцатым переключимся на динамичный метод. Таким образом, играя с 3-го по 16-й кон, мы каждый раз делим наш капитал на части по двадцать долларов и ставим на кон столько долларов, сколько получилось таких частей, то есть действуем по методу статичного дробления f.
Итак, предположим, что после второго кона на нашем счете имеется 210 долл. На следующий кон мы поставили бы десять долларов (так как 210/20 = 10,5, а ближайшее целое – 10). Так же мы будем действовать каждый следующий кон до шестнадцатого включительно.
На семнадцатом кону мы можем видеть, что градиент динамичного f выше других. Поэтому мы должны переключиться на игру на основе динамичного f. И вот как именно. Когда мы начинали, мы решили играть активным капиталом в 20% счета (так как мы решили играть одной пятой всего оптимального f). Поскольку наш исходный счет составлял 200 долларов, мы начали первый кон с 40 долларов активной части счета. Значит, пассивная часть счета составляла бы 160 долларов.
Таким образом, перед началом 17-го кона, на котором мы хотим переключиться на динамический метод, мы вычитаем 160 долларов из всего того, что есть на нашем счете. Полученную разность мы далее делим на части по 4 доллара, или на оптимальное f$, и получаем в итоге величину ставки, которую можно сделать в 17-м коне. Продолжаем действовать таким образом перед каждым коном до бесконечности.
Предположим, что на нашем счете после 16-го кона имеется 292 доллара. Вычитая из этого 160 долларов, получаем 132, деля которые на 4 доллара, приходим к величине 33. То есть в 17-м коне мы можем сделать 33 ставки по 1 доллару (или одну ставку в 33 доллара).
Если хотите, то вы также можете представить эти точки перелома при постоянном доминировании в виде прироста процента выигрыша, который необходимо иметь до перехода на следующий уровень. Поскольку формула [5.13] дает нам вертикальную координату, или Y, соответствующую горизонтальной координате из формулы [5.09], то мы можем определить вертикальные координаты, соответствующие формулам [5.18– 20]. Так как вы переключаетесь с постоянной ставки на статичное f при таком значении Т, на котором [5.19] больше, чем [5.16], то вы можете подставить это Т в [5.16] и вычесть из результата 1. Это будет процентный прирост на ваш начальный капитал, который нужен для перехода с постоянной ставки на статичное f.
Так как вы переключаетесь на динамичное f при таком значении Т, на котором [5.20] больше, чем [5.CAPut!'], то вы, следовательно, можете подставить это Т в [5.16] и вычесть из результата 1, что и и будет процентом прибыли на начальный капитал для перехода к игре на основе динамичного f.
|