6.4.4. Свойства портфеля ценных бумаг

Свойства портфеля ценных бумаг ниже иллюстрируются в зависимости от отсутствия или же наличия корреляции между ценными бумагами, входящими в портфель.

а) Отсутствие корреляции между ценными бумагами, входящими в портфель

Предположим, что эффекты от различных видов ценных бумаг, входящих в портфель, взаимно независимы, что математически эквивалентно отсутствию корреляции между ценными бумагами, то есть V_{i, j} = 0 при i = j.

Тогда дисперсия эффективности портфеля определится как:

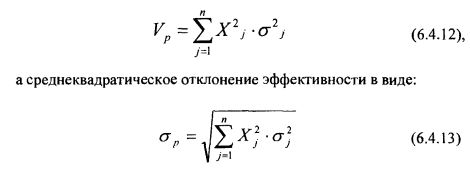
Предположим далее, что инвестор вложил свои средства равными долями во все ценные бумаги. Тогда X_j = 1/п и инвестор получит средний ожидаемый эффект в виде:

Переходя к пределу в выражении (6.4.17), получим:

Из выражения (6.4.18) следует, что при ограниченности среднеквадратического отклонения эффективности ценных бумаг, входящих в портфель, риск портфеля ограничен и стремится к нулю при неограниченном возрастании числа ценных бумаг в портфеле. Отсюда проистекают рекомендации для инвесторов о целесообразности диверсификации портфеля, то есть необходимости составлять портфель из возможно большего числа взаимнонекоррелированных ценных бумаг.

б) Положительная взаимная корреляция между ценными бумагами, входящими в портфель

Напомним, что дисперсия эффективности портфеля или же его риск определяется формулой (6.4.11) т.е.:

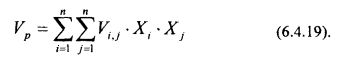
С учетом того, что коэффициент корреляции для 2-х случайных величин определяется формулой:

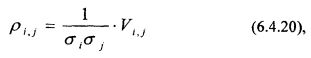
формулу (6.4.19) для риска портфеля можно представить в виде:

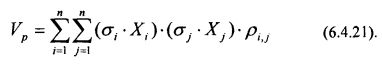
Рассмотрим далее случай положительной корреляции, когда ρ_{i, j} = 1. Тогда, с учетом (6.4.21), выражение для риска портфеля можно записать в виде:

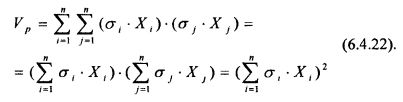
Рассмотрим далее эффективность простой диверсификации ценных бумаг в портфеле в условиях прямой положительной корреляции между ценными бумагами. Будем считать, что первичные средства распределены в равных долях, т. е. X_i = 1/n. Тогда, с учетом (6.4.22), выражения для дисперсии эффективности (риска) портфеля и его среднеквадратического отклонения будут иметь вид:

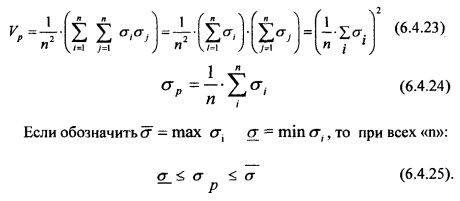
При полной (то есть единичной) положительной корреляции между ценными бумагами диверсификация портфеля не даёт положительного эффекта. В этом случае, в соответствии с выражением (6.4.25), среднеквадратическое отклонение эффективности (то есть среднеквадратическое значение «риска») портфеля просто равно среднему риску от отдельных вложений и не стремится к нулю с увеличением числа ценных бумаг. По содержательному смыслу положительная корреляция имеет место, когда движение курсов ценных бумаг определяется действием одного и того же фактора, и это действие проявляется в движении курсов в одну и туже сторону.

в) Отрицательная взаимная корреляция между ценными бумагами, входящими в портфель

Для уяснения сути вопроса рассмотрим случай полной обратной корреляции между ценными бумагами, входящими в портфель, то есть когда коэффициент корреляции ρ_{i, j} = -1 при (i ≠ j). Далее ограничимся рассмотрением случая 2-х ценных бумаг, который без труда можно обобщить на любое число ценных бумаг, включаемых в портфель.

С учетом формулы (6.4.21), будем иметь:

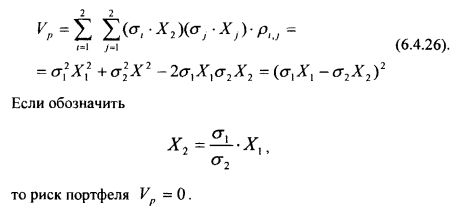
Это означает, что в случае полной обратной корреляции между ценными бумагами, входящими в портфель, можно выбрать такие пропорции между ними, что риск портфеля будет полностью отсутствовать.

По содержательному смыслу полная обратная корреляция между ценными бумагами, входящими в портфель, означает, что движение их курсов осуществляется в противоположных направлениях.

На практике наиболее реальными являются ситуации, когда нет полной прямой или же обратной корреляции между ценными бумагами, однако разумная диверсификация портфеля может привести к снижению риска портфеля без потери его эффективности.

Содержание

Далее