2.13. Приложение: ожидаемая полезность и Петербургский парадокс
Рассуждение, известное как “Петербургский парадокс”, было изложено в статье Даниила Бернулли, представленной в 1738 г. Императорской Академии наук в Петербурге. Проблема была сформулирована следующим образом:
“Петр бросает монету раз за разом, пока она не выпадет “орлом”. Он обязуется выплатить Павлу один дукат, если “орел” выпадет при первом бросании, два дуката – если при втором, четыре – если при третьем, восемь – если при четвертом и так далее, так что каждый неудачный бросок удваивает величину платежа. Предположим, что мы хотим определить ожидаемый результат Павла”.
Ожидаемый платеж может быть вычислен как сумма возможных платежей, умноженных на их вероятности:
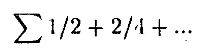
При любом конечном числе бросаний п получается сумма п/2, а при п → ∞ она становится бесконечной. Следовательно, если исходить из математического ожидания, Павел должен быть готов заплатить бесконечную цену за право участия в такой игре. Тем не менее мало кто согласится с таким выводом, несмотря на быстрый рост выплат в случае длинной серии “решеток”.


В попытках разрешить этот парадокс (Крамером, а затем самим Бернулли) было выработано понятие “полезности” денег. Крамер предположил, что полезность растет медленнее, чем сама величина платежа. В независимо предположенном решении Бернулли маргинальная полезность денег была принята обратно пропорциональной имеющемуся капиталу.
Этот пример имеет прямое отношение к современной финансовой теории, поскольку в нем обсуждается, сколько следует платить за обладание рисковым активом. В принятии инвестиционных решений всегда можно выделить следующие этапы: описание доступных инвестиционных возможностей; оценка для каждого варианта величины, сроков и надежности будущих платежей; оценка капитальных затрат для каждого варианта; наконец, окончательная оценка каждого варианта с учетом индивидуального отношения к риску. Петербургский парадокс может рассматриваться как частный случай такой оценки рискового инвестирования.
Один способ общего решения проблемы предложен теорией ожидаемой полезности. Эта теория постулирует, что если x(s) – это платеж, ассоциированный с каким-то инвестиционным проектом, в состоянии s, a π(s) – это вероятность реализации состояния s, то “истинная ценность” проекта для инвестора равна
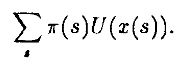
В ситуации Петербургского парадокса s соответствует бесконечной последовательности “орлов” и “решеток”, a x(s) означает платеж, полагающийся при реализации этой последовательности. Парадокс возникает, если U(x(s)) = x(s), т. е. “ценность” просто равна ожидаемому платежу. Если же функция U ограничена, то ожидаемая полезность будет конечной.
Для наших целей достаточно просто принять гипотезу, что все инвестиционные решения оцениваются ожидаемой полезностью. В формальной же теории исходят из индивидуальных предпочтений на множестве стохастических исходов, а затем изучают условия, при которых эти предпочтения действительно могут быть описаны с помощью функции полезности.
|