4.6. Арбитраж и эффективность рынка

Гипотеза об эффективности рынка занимает фундаментальное положение в теории финансов, поэтому значительные усилия направляются на изучение взаимосвязи между информированностью и ценами. Фактически мы до сих пор не обсуждали механизм агрегирования информации в ценах. Например, если часть трейдеров знает, что в будущем цена акции будет либо 0, либо 25, а другие знают, что случится 0 или 45, то модель рациональных ожиданий предсказывает, что цена равна 0. Однако модель рациональных ожиданий ничего не говорит о том, как цены упадут до нуля. Если все состояния равновероятны, то в данном примере весьма правдоподобно, что цены будут колебаться вблизи 20, поскольку это ожидаемая стоимость для одной группы трейдеров и одна из возможных стоимостей для другой группы. Объяснение реакции цен на информированность является одной из наиболее сложных проблем, возникающих перед участниками рынка. Здесь, па относительно простом примере, мы покажем, что если на рынке имеется достаточно много производных ценных бумаг (в частности, опционов), то, если рынок неэффективен, кто-либо из трейдеров будет обладать возможностями для арбитража. Это сильный аргумент в пользу эффективности. Напомним, что возможность арбитража означает, что трейдер может получить чистый доход без каких-либо расходов.

В нашем обсуждении роли опционов для эффективности рынка мы будем использовать следующий пример. Имеется один вид акций, и стоимость акции в будущем задастся таблицей:

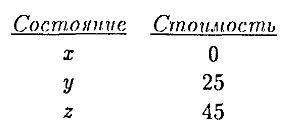
Помимо акций на рынке обращаются колл-опционы с ценой исполнения 30 и пут-опционы с ценой исполнения 30, оба сроком на один период. Для того, чтобы еще больше упростить пример, предположим, что безрисковый процент равен пулю (в противном случае нам следовало бы дисконтировать все будущие платежи на безрисковый процент).

Предположим, что истинным является состояние х и некоторые трейдеры (типа T1) знают, что истинное состояние “не y”, другие (типа T2) знают, что истинное состояние “не z”.

В равновесии при рациональных ожиданиях (REE) цена акции равна 0, а цены опционов в таком равновесии вычисляются следующим образом. Как мы знаем из раздела, посвященного опционам, колл-опцион должен иметь цену С – max{0, S – 30}, а пут-опцион – цену Р = max{0, 30 – S}, где S – цена акции. Таким образом, REE-цена колл-опциона равна 0 и REE-цена пут-опциона равна 30. Заметим, что эти цены основаны на понятии равновесия при рациональных ожиданиях, что в данном случае означает, что нет никакой неопределенности, поскольку цена акции выявила всю наличную информацию.

Чтобы увидеть роль производных бумаг для эффективности рынка, рассмотрим два типа трейдеров и их информированность:

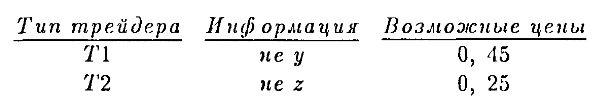
Рассмотрим портфель, состоящий из +1 акции и –3 колл-опционов. Пусть S означает цену акции, С – цену колл-опциона и Р – цену пут-опциона. Тогда для трейдера типа T1 этот портфель приносит 0 независимо от того, будет цена акции 0 или 45. Отсутствие арбитража требует, чтобы цена портфеля равнялась нулю, т. е. S – 3C = 0. Если S – 3C < 0, то трейдер типа 21 должен купить столько портфелей, сколько возможно, поскольку он получит доход при покупке, а потери в конце периода, будут равны нулю. Аналогично, если S – 3C > 0, то трейдер T1 должен продавать сколько возможно.

Трейдер T2 знает, что колл-опцион ничего не принесет (поскольку цена исполнения равна 30), так что мы получаем С = 0. Вместе эти два ограничения дают S = 0, С = 0. Чтобы определить цену пут-опциона, используем взаимосвязь “пут–колл” (это соотношение обсуждалось в разделе, посвященном опционам): S + Р – С + 30, откуда получаем Р = 30.

Заметим, что требование отсутствия арбитража реально накладывает ограничения па цены покупки и продажи (биды и аски), поскольку единственный способ получить арбитражный выигрыш – это принять имеющийся бид или аск. Таким образом, отсутствие арбитража подразумевает, что

1. S^α – 3C^b ≥ 0, так что трейдер Т1 не может купить такой портфель по отрицательной цене,

2. S^b – 3C^α ≤ 0, так что трейдер T1 не может продать такой портфель по положительной цене,

3. С^b ≤ 0, так что трейдер T2 не может продать колл-опцион но положительной цене,

4. C^α ≥ 0, так что трейдер Т2 не может купить колл-опцион по отрицательной цене.

Поскольку биды и аски должны быть неотрицательны, условие 3 сводится к С^b = 0, а условие 4 является несущественным.

В этом примере мы обратились к двум портфелям: S – 3C = 0 и C = 0, называемым “сепарирующими”, поскольку они разделяют информацию двух типов трейдеров. Оказывается, что для каждого из трех состояний отсутствие арбитража влечет рациональные ожидания. Сепарирующие портфели для двух типов трейдеров приведены в таблицах:

Связь между арбитражем и эффективностью легко видна на графике. Например, если истинное состояние z, мы можем нарисовать графики уравнений сепарирующих портфелей:

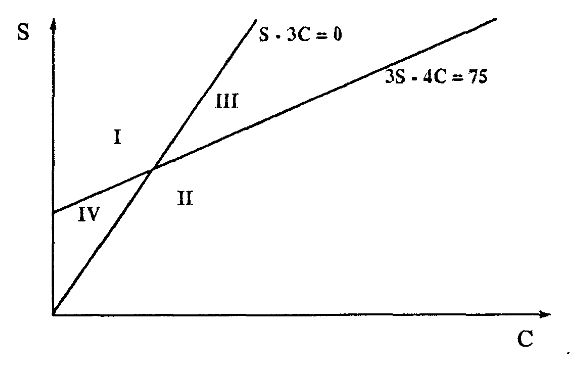
На этом рисунке трейдер типа Т1 захочет купить любой такой портфель, что S^α – 3C^b < 0, и продать, если S^b – 3C^α > 0. Аналогичное утверждение относится к трейдера типа Т2. Это означает, что мы не будем наблюдать какие-либо комбинации бидов на акцию/асков на колл-опцион в области, помеченной I, и не будем наблюдать комбинации асков на акцию/бидов на колл-опцион в области, помеченной II. В областях III и IV трейдеры одного типа захотят осуществить покупку, а другого – продажу. Однако поскольку желаемые соотношения между акциями и колл-опционами различны для разных групп, такая ситуация не может сохраняться.

Особенно простой случай сепарирования возникает для состояния y. Здесь для агрегирования информации достаточно границ на цены акций, поскольку трейдерам тина T1 известно, что S ≥ 25, а трейдерам типа T2 – что S ≤ 25. Таким образом, минимально возможная стоимость для типа Т2 является максимально возможной для типа T1. В общем случае, если портфель является сепарирующим, то он может быть охарактеризован в терминах минимального и максимального платежей. Пусть min_i обозначает минимальный платеж по портфелю при имеющейся у трейдера i информации, а max_i, обозначает соответствующий максимальный платеж. Тогда портфель сепарирует в том и только в том случае, когда

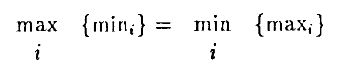
Эти рассуждения не будут иметь места, если количество опционов недостаточно. В предельном случае, если опционов пет вовсе, требование отсутствия арбитража почти не ограничивает цены.

Содержание

Далее