1.1. Риск, связанный с изменением процентной ставки, и теорема об иммунитете облигаций
Одним из способов контроля риска при изменении цен облигаций в связи с изменением процентных ставок (процентный риск), или хеджирования (hedging) риска, является управление дюрацией портфеля облигаций и использование теоремы об иммунитете. Понятие "дюрация" (duration) было впервые введено Макколи и характеризует чувствительность стоимости облигаций к изменению процентных ставок. Ниже мы временно опустим индексы при r для упрощения обозначений. Пусть r обозначает доходность облигации к погашению, тогда r удовлетворяет уравнению:
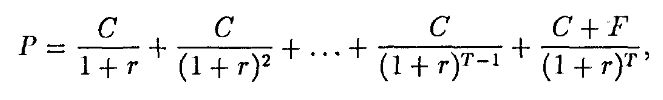
где С – выплата по купону, F – номинальная стоимость облигации, Т – срок погашения и Р – текущая цена облигации. Перепишем равенство:
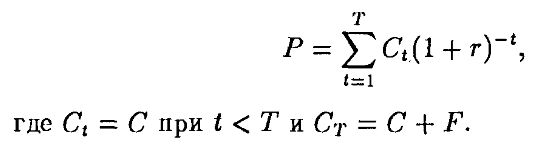
Тогда можно записать
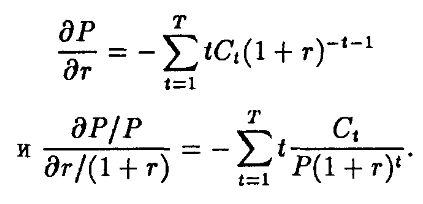
Формально левая часть равенства является эластичностью цены облигации по отношению к (1 + r) и характеризует процентное изменение цены облигации по сравнению с процентным изменением (1 + r). Но есть и другая интерпретация. Заметим, что Ct(1 + r)-t-1 является текущей стоимостью платежа в периоде t. Поскольку
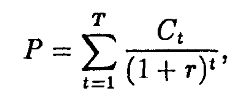
то
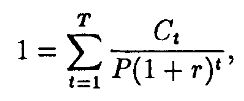
и
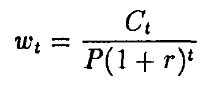
является долей цены, которую вносит платеж в момент времени t.
Теперь мы можем переписать то же равенство как
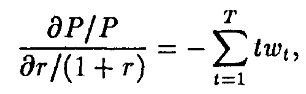
и поскольку
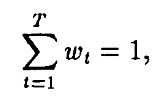
эта эластичность равна средневзвешенному времени погашения с весами wt. Тогда определим дюрацию Макколи так:
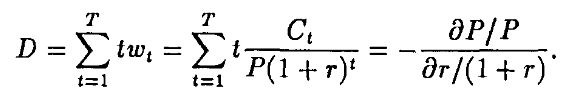
Отметим, что дюрация бескупонной облигации в точности равна времени погашения, в то время как для купонной облигации она меньше этого времени.


Поскольку дюрация характеризует чувствительность цены облигации, или, в более общем смысле, потока платежей, к изменению доходности к погашению, мы можем пытаться управлять риском, связанным с изменением процентной ставки, используя дюрацию. Например, предположим, что вы должны заплатить $1000 ровно через два года. Тогда дюрация вашей задолженности равна 2. Одним из способов защиты от изменения процентных ставок является покупка бескупонной облигации с номинальной стоимостью $1000, погашаемой через два года. Если 0r2 – процентная ставка на два года, то эта покупка обойдется вам в 1000/(1 + 0r2)2 и ваши обязательства будут в точности соответствовать вашим активам.
Теорема об иммунитете (впервые получена Самуэльсоном) утверждает, что риск, связанный с изменением процентных ставок, можно хеджировать, выравнивая дюрации активов и задолженностей. Это правило основано на том факте, что процентный риск возрастает с уменьшением цены облигации и, наоборот, уменьшается с увеличением цены, и что облигации с разными сроками погашения реагируют по-разному на изменения процентных ставок. В результате, если процентная ставка растет, доход от реинвестиции купонов возрастает, но рыночная стоимость облигации падает, и наоборот, если процентная ставка падает, то стоимость облигации растет. Проиллюстрируем это правило на примере простого обязательства выплатить $С в момент времени t. Тогда текущая стоимость задолженности равна
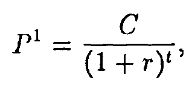
и дюрация равна t. Назовем такую задолженность облигацией 1. Рассмотрим две бескупонные облигации с номинальными стоимостями C1 и С2 и временами погашения t1 и t2 соответственно. Тогда
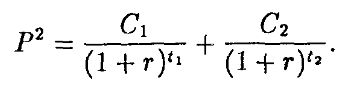
Портфель из двух таких облигаций назовем облигацией 2. Предположим, что
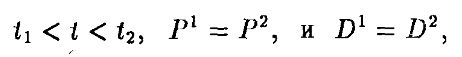
где D1 и D2 – дюрации облигаций 1 и 2 соответственно.
Пример
Рассмотрим текущую стоимость как функцию процентной ставки для двух потоков платежей:
Альтернатива А:
В конце года 10 платеж равен $109. Других платежей нет.
Альтернатива Б:
В конце года 2 платеж равен $22, а в конце года 18 – $135. Других платежей нет.
Альтернатива А имеет дюрацию 10. Если процентная ставка равна 12%, то дюрация альтернативы Б также равна 10. Заметим, что хотя дюрация каждой из компонент альтернативы Б известна (2 и 18 соответственно), мы не можем определить дюрацию этого потока платежей в совокупности, не делая предположений о процентной ставке. При ставке 12% оба этих потока платежей имеют одинаковую текущую стоимость. Текущая стоимость (ТС) как функция процентной ставки определяется следующей таблицей:
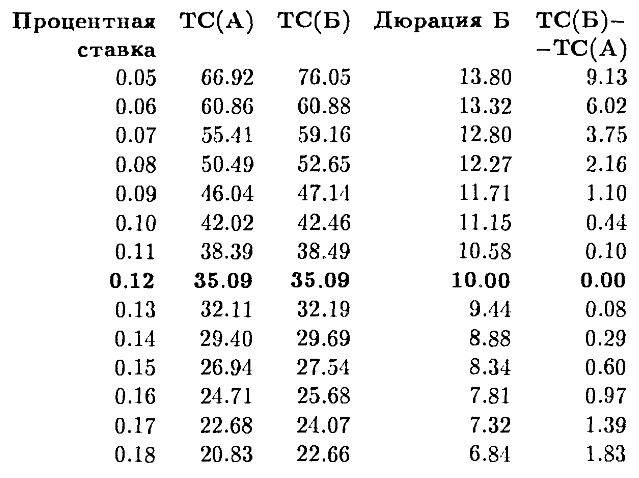
Отмстим, что текущие стоимости равны при 12% (когда равны дюрации), а при любых других процентных ставках альтернатива Б всегда более ценна, чем альтернатива А.
Покажем, что соотношение между стоимостью облигаций и доходностью к погашению, продемонстрированное на этом примере, имеет общий характер.
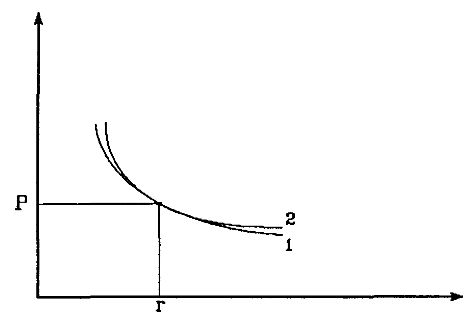
Таким образом, когда доходность к погашению возрастает, текущая стоимость задолженности падает сильнее, чем текущая стоимость облигации 2, в то время как, если доходность падает, то стоимость задолженности растет медленнее, чем стоимость облигации 2. Поэтому облигация 2 “защищает” задолженность. Доказательство заключается в следующем. Мы знаем, что эти две облигации имеют одинаковые стоимости и одинаковые дюрации при ставке r. Это означает, что две кривые должны касаться в точке (r, P). Известно также, что цена убывает при возрастании доходности, поэтому обе кривые наклонены вниз. Теперь покажем, что вторая производная для первой кривой меньше, чем для второй кривой при равной дюрации. Значит, кривые касаются в точке (r, Р), причем вторая лежит выше первой, что и показано на рисунке:
Результат для вторых производных вытекает из неравенства Йенсена следующим образом:
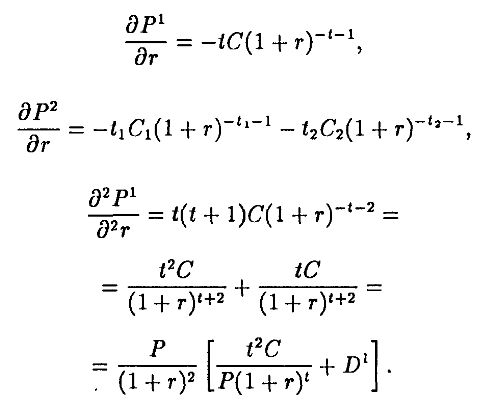
Аналогично
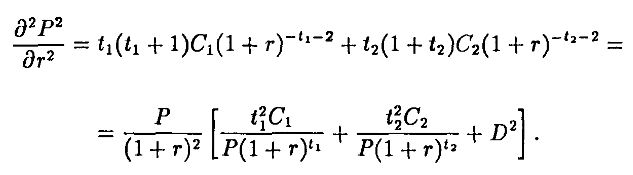
Для того чтобы увидеть, что первое выражение превосходит второе, вспомним определение дюрации, обозначив
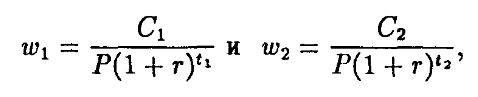
w1 + w2 = 1 и, поскольку дюрации двух облигаций равны, получим
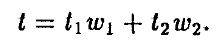
Поэтому, если нам удастся показать, что t2 < w1t12 + w2t22, мы докажем, что вторая производная облигации 1 меньше, чем вторая производная для облигации 2. Это следует из неравенства Йенсена и того, что t2 – выпуклая функция. Неравенство Йенсена утверждает, что если f(x) – строго выпуклая функция, то f(αx1 + (1 – α)x2) < αf(x1) + (1 – α)f(x2). Обозначив α = w1, 1 – α = w2 и x = t, получим требуемый результат.
Рисунок также показывает, что мы не получим точную меру чувствительности к изменению процентных ставок простым вычислением и. На рисунке обе облигации имеют одинаковые дюрации, но облигация 2 более чувствительна. Зависимость цены от процентной ставки для облигации 2 – “более выпуклая”, что показывает вычисление второй производной. Вообще более выпуклая зависимость лучше менее выпуклой. Меру выпуклости характеризует вторая производная, обычно нормализованная либо на цену облигации, либо на удвоенную цену.
Теорема об иммунитете опирается на нереалистическое предположение об изменениях процентных ставок, а именно на то, что изменение доходности не зависит от времени погашения. Например, если доходность одномесячных казначейских векселей изменилась на 5 базисных пунктов (1/100 процента равна 1 базисному пункту), то и доходность тридцатилетних правительственных облигаций должна измениться на 5 базисных пунктов. Это предположение нереалистично, потому что допускает только параллельные сдвиги во временной структуре процентных ставок. Однако существует другой подход к управлению процентным риском. Для этого нужны дополнительные рынки, называемые форвардными рынками, которые позволяют торговать непосредственно риском.
|