4. Вега
Определение веги
Вега измеряет чувствительность цены опциона к изменению волатильности. Другими словами, параметры вега и дельта являются сестрами. Одна измеряет чувствительность премии к цене спот, а другая — к волатильности.
Вега выражается в процентах. Стоимость опциона с вегой 0,04% увеличится на 0,04%, если волатильность увеличится на 1%. Например, если вы купили опцион на $1 млн за $1000 и его вега равна 0,0025%, а затем волатильность увеличилась на 1%, то цена опциона увеличится до $1,025 млн.
«Короткая» и «длинная» вега
Существует правило, что цены краткосрочных опционов менее чувствительны к изменениям волатильности, чем цены долгосрочных опционов (они имеют более низкую вегу), а вега опционов с маленькой дельтой ниже, чем с большой.
На рыночном жаргоне это звучит так: если позиция зарабатывает на росте волатильности, она называется длинной на вегу (long vega), а если при увеличении волатильности ее стоимость уменьшается, то — короткой на вегу (short vega).
Поведение веги
Долгосрочные опционы не очень чувствительны к изменениям цен базового актива и скорость амортизации их премий незначительна, однако они чрезвычайно восприимчивы к изменениям волатильности. Их вега имеет большее абсолютное значение, чем у краткосрочных опционов (например, atm-опционы с одним номиналом, но с разными сроками истечения). Поскольку краткосрочные опционы имеют низкую вегу, изменение волатильности оказывает относительно незначительное влияние на их стоимость.


Покупатели опционов выигрывают, если волатильность растет. Продавцы опционов («продавцы веги») выигрывают, если волатильность падает.
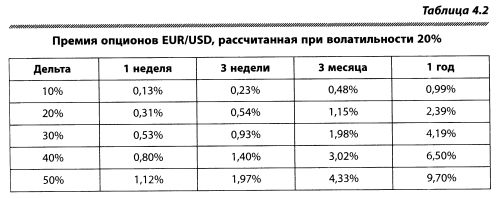
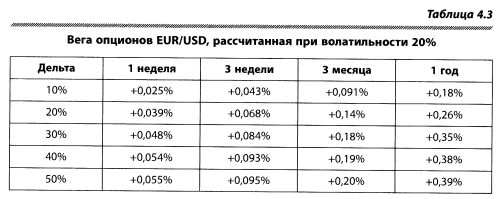
Итак (таблицы 4.2 и 4.3),
— в то время как долгосрочные опционы нечувствительны к изменениям курса спот или к увяданию времени (это понятие рассматривается в параграфе, посвященном тете), они очень восприимчивы к изменениям волатильности. Их вега имеет большее абсолютное значение;
— краткосрочные опционы имеют низкую вегу, и изменение волатильности оказывает относительно незначительное влияние на их стоимость;
— для покупателей опционов вега служит позитивным фактором, и они выигрывают, если волатильность растет;
— для продавцов опционов вега служит негативным фактором, и они выигрывают, если волатильность падает.
Использование смайлов и skew
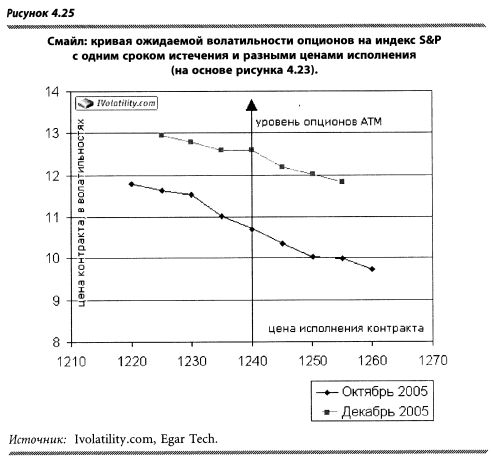
Эта тема больше интересна читателям, которые уже освоили базовые знания по волатильности и веге. Смайл — это премия или дисконт, выраженные в волатильностях за otm и itm (опционы «без денег» и «при деньгах») по сравнению с atm, для опционов с одной датой истечения (рисунок 4.25). Как правило, премию платят за опционы в направлении цен, в котором ожидается большая волатильность. Например, на рынке S&P рост волатильности происходит, когда рынок падает. Поэтому цены в волатильностях на otm S&P путы (например, 20-дельтовый пут — 14,5 волатильности) выше, чем atm-путы (например, 14 волатильностей). Для 1100 пут, истекающего в октябре, эквивалентом 14,50% в центах будет 6, а не 5, соответствующих 14%, т. е. трейдер «заработает» 1 цент. Это слово пишется в кавычках, т. к. прибыль превратится из теоретической в реальную только по истечении опциона.
При этом величина премии в волатильностях (цена, выраженная в волатильностях) над atm различна для опционов с разной дельтой. Так, премия 20-дельтового пута — 0,5% над ценой atm, а премия 30-дельтового пута — 0,4% над ценой atm. Размер корректировки премии опционов каждой дельты определяется с помощью skew. В большинстве ситуаций значения skew и smile устанавливаются рынком «на глазок».
Приложение смайлов представляет для маркетмейкеров исключительный интерес, т. к. большинство из них используют его в управлении позиционными рисками. Сама концепция возникла, и не в последнюю очередь, из-за злоупотреблений со стороны трейдеров. Ее суть заключается в следующем: поскольку волатильность опционов «при своих» (atm) часто отличается от волатильности опционов «без денег» (otm), трейдеры злоупотребляют продажами последних. Это происходит в том случае, если переоценка захеджированного портфеля (позиции) базируется на ценах на опционы «при своих» (atm). Продав по более высокой волатильности опционы «без денег», трейдеры получают «теоретическую» прибыль в размере разницы волатильности опционов «при деньгах» и «вне денег», т.е. в размере skew.
Для борьбы с этим явлением была введена более сложная система, оценивающая волатильности каждой дельты отдельно, а не волатильности опционов с 50%-ной дельтой (atm). Например, если волатильность опциона с дельтой 20 выше волатильности опционов с 50%-ной дельтой, он будет оценен по собственной волатильности.
Такая система избавляет от неправильной переоценки портфеля, но вместе с тем создает ряд проблем. Во-первых, меняется дельта (дельта опциона, оцененная по разной волатильности, — разная). Во-вторых, появляется ее некая непредсказуемость — при единообразной волатильности можно говорить о предсказуемой гамме (параметр рассматривается позже): на единицу движения спота дельта меняется в определенной пропорции. В случае с разными степенями волатильности, соответствующими разным дельтам, появляется некоторый элемент «кривой», т.к. на гамму действует дополнительный фактор — изменение волатильности в дополнение к изменению спота. Эти факторы влекут за собой разные потребности хеджирования для двух методов переоценки.
В-третьих, смайл порождает и другую проблему — меньшую предсказуемость результатов ввиду несоответствия между предсказанной им и реальной волатильностью. Известно, что смайл используют как индикатор рыночного предсказания уровня волатильности, когда спот дойдет до конкретного ценового уровня. Например, премия 20-дельтового пута — 0,5% над ценой atm предполагает, что когда спот дойдет до страйка пута и он из otm превратится в atm, уровень atm волатильности будет на 0,5% выше, чем сегодня.
Следующий пример продемонстрирует, каким образом изначальный учет смайла потенциально деформирует результаты. Предположим, что при курсе USD/JPY 110,00 волатильность трехмесячного 50-дельтового опциона равна 14%, а волатильность 20-дельтового с ценой исполнения 107,00 — 15%. Другими словами, 20-дельтовый продается с премией в 1% к 50-дельтовому. Это означает, что рынок опционов ожидает рост волатильности при движении курса доллара вниз. Предположим, что через месяц рынок спустился до уровня 107,00 и волатильность двухмесячных опционов стала равна 13%. Получается, если бы маркетмейкер первоначально оценил этот опцион по 14%, то колебания переоценки книги были бы меньше, а в данном случае придется снижать ее с 15 до 13%.
Таким образом, принимая решение использовать смайл для переоценки стоимости позиции, трейдер должен отдавать себе отчет в том, что, получая более справедливую оценку результата в момент проведения сделки, он увеличивает размеры неточности в хеджировании и в предсказуемости результатов.
Вышеизложенное поможет вам ответить на следующие вопросы:
1. Основываясь на таблице 4.3, определите, как изменится цена 1-недельного опциона с дельтой 20%, когда волатильность увеличится на 1%?
0, 349 = 0,31 + 0,039
2. Какая математическая взаимосвязь между вегами опционов с дельтой 50 и 20 со сроками:
— 1 неделя;
— 3 недели;
— 3 месяца?
Около 1,4 для всех сроков.
3. Какая математическая взаимосвязь между премиями опционов с дельтой 50 и 20 со сроками:
— 1 неделя;
— 3 недели;
— 1 год?
Около 2 со всеми дельтами.
4. Какой вывод вы можете сделать о взаимосвязи премий и параметров вега исходя из соотношений, приведенных в вопросах 2 и 3?
5. Какова взаимосвязь параметров вега у опционов с дельтой 50 со сроками:
— 1-недельный к 3-недельному;
— 3-недельный к 3-месячному;
— 3-месячный к 1-летнему?
6. Какова взаимосвязь премий опционов с дельтой 50 со сроками:
— 1-недельный к 3-недельному;
— 3-недельный к 3-месячному;
— 3-месячный к 1-летнему?
7. Какой вывод вы можете сделать о взаимосвязи премий с дельтой 50 и параметров вега исходя из соотношений, приведенных в вопросах
5 и 6?
Вега:
— взаимосвязь параметров вега опционов с дельтой 50 и 20 устойчива для всех сроков;
— вега долгосрочных опционов выше, в то время как отношение дельт может быть 50 к 20 (2,5), а отношение параметров вега — около 1,4; иными словами, отношение дельты к веге составляет около 1,8, а не 1.
Премия:
— все то же самое, только другие отношения.
8. Вашему клиенту нужен совет: что дешевле — купить 1-летний опцион или четыре раза покупать 3-месячный. Что вы думаете по
этому поводу?
Помните о взаимосвязи параметров веги и премий опционов с той же дельтой и разными сроками! Один 1-летний опцион примерно равен по стоимости двум 3-месячным опционам. Таким образом, один 1-летний опцион дешевле, чем четыре 3-месячных.
9. Волатильность очень высокая, и вы ожидаете, что она резко снизится. Ваш клиент хочет купить опцион, но выбирает между 2-месячным
и 4-месячным. Что вы ему посоветуете?
Купить 2-месячный опцион, т.к. он менее чувствителен к снижению волатильности.
|